
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 376 Атанасян — Подробные Ответы
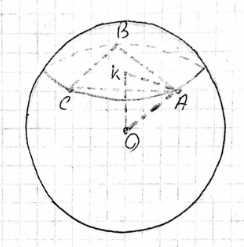
Вершины треугольника АВС лежат на сфере радиуса 13 см. Найдите расстояние от центра сферы до плоскости треугольника, если \(АВ = 6\) см, \(ВС = 8\) см, \(АС = 10\) см.
Плоскость треугольника ABC пересекает сферу с центром O по окружности, описанной около треугольника ABC. OK — расстояние от центра сферы до плоскости треугольника, где K — центр описанной окружности треугольника ABC. OK перпендикулярен плоскости ABC. Треугольник OKA — прямоугольный с прямым углом при K. По теореме Пифагора: \(OK = \sqrt{OA^2 — KA^2}\). Радиус сферы \(OA = R = 13\), поэтому \(OK = \sqrt{13^2 — AK^2}\). Длина AK — это радиус описанной окружности треугольника ABC. \(AK = \frac{AB \cdot BC \cdot CA}{4 \cdot S_{ABC}}\). Найдем полупериметр треугольника ABC: \(p = \frac{6+8+10}{2} = 12\). Найдем площадь треугольника ABC по формуле Герона: \(S_{ABC} = \sqrt{12(12-6)(12-8)(12-10)} = \sqrt{12 \cdot 6 \cdot 4 \cdot 2} = \sqrt{576} = 24\). Найдем радиус описанной окружности AK: \(AK = \frac{6 \cdot 8 \cdot 10}{4 \cdot 24} = \frac{480}{96} = 5\). Найдем OK: \(OK = \sqrt{13^2 — 5^2} = \sqrt{169 — 25} = \sqrt{144} = 12\). Расстояние от центра сферы до плоскости треугольника равно 12 см.
Плоскость, в которой лежит треугольник ABC, пересекает сферу с центром O по окружности. Поскольку вершины треугольника ABC лежат на сфере, эта окружность является описанной окружностью для треугольника ABC. Расстояние от центра сферы O до плоскости треугольника ABC — это длина перпендикуляра, опущенного из точки O на эту плоскость. Основание этого перпендикуляра, точка K, будет центром описанной окружности треугольника ABC. Таким образом, искомое расстояние равно длине отрезка OK.
Соединим центр сферы O с одной из вершин треугольника, например, с вершиной A. Отрезок OA является радиусом сферы, заданным как \(R = 13\) см. Отрезок KA является радиусом описанной окружности треугольника ABC. Поскольку OK перпендикулярен плоскости треугольника ABC, он перпендикулярен любой прямой, лежащей в этой плоскости и проходящей через его основание K, в частности, отрезку KA. Следовательно, треугольник OKA является прямоугольным с прямым углом при вершине K.
Применяя теорему Пифагора к прямоугольному треугольнику OKA, получаем соотношение: \(OK^2 + KA^2 = OA^2\). Из этого следует, что искомое расстояние \(OK = \sqrt{OA^2 — KA^2}\). Нам известен радиус сферы \(OA = 13\) см. Для нахождения OK необходимо вычислить длину радиуса описанной окружности треугольника ABC, то есть длину отрезка KA.
Радиус описанной окружности KA для треугольника ABC со сторонами AB, BC, AC и площадью \(S_{ABC}\) может быть найден по формуле: \(KA = \frac{AB \cdot BC \cdot AC}{4 \cdot S_{ABC}}\). Нам известны длины сторон треугольника: \(AB = 6\) см, \(BC = 8\) см, \(AC = 10\) см. Для применения этой формулы сначала нужно найти площадь треугольника ABC.
Площадь треугольника ABC можно вычислить по формуле Герона, поскольку известны длины всех трех сторон. Сначала найдем полупериметр \(p\) треугольника: \(p = \frac{AB + BC + AC}{2} = \frac{6 + 8 + 10}{2} = \frac{24}{2} = 12\) см.
Теперь вычислим площадь \(S_{ABC}\) по формуле Герона: \(S_{ABC} = \sqrt{p(p-AB)(p-BC)(p-AC)} = \sqrt{12(12-6)(12-8)} \cdot\)
\( \cdot\sqrt{(12-10)} = \sqrt{12 \cdot 6 \cdot 4 \cdot 2}\). Вычислим произведение под корнем: \(12 \cdot 6 \cdot 4 \cdot 2 = 72 \cdot 8 = 576\). Таким образом, \(S_{ABC} = \sqrt{576} = 24\) кв. см.
Теперь, зная длины сторон и площадь треугольника ABC, мы можем найти радиус описанной окружности KA: \(KA = \frac{6 \cdot 8 \cdot 10}{4 \cdot 24} = \frac{480}{96}\). Выполним деление: \(480 \div 96 = 5\). Следовательно, радиус описанной окружности \(KA = 5\) см.
Наконец, подставим значения OA и KA в формулу для OK, полученную из теоремы Пифагора: \(OK = \sqrt{OA^2 — KA^2} = \sqrt{13^2 — 5^2} = \sqrt{169 — 25} = \sqrt{144}\). Извлекаем квадратный корень: \(\sqrt{144} = 12\).
Таким образом, расстояние от центра сферы до плоскости треугольника ABC равно 12 см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!