Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 375 Атанасян — Подробные Ответы
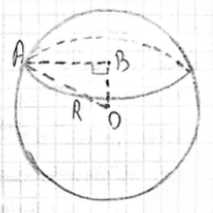
Шар радиуса 41 дм пересечён плоскостью, находящейся на расстоянии 9 дм от центра шара. Найдите площадь сечения.
Сечение шара плоскостью является кругом. Радиус этого круга \(AB\) можно найти по теореме Пифагора: \(AB = \sqrt{R^2 — OB^2}\). Подставляя данные значения, получаем \(AB = \sqrt{41^2 — 9^2} = \sqrt{1681 — 81} = \sqrt{1600} = 40\) дм. Площадь круга в сечении находится по формуле \(S = \pi \cdot AB^2\). Следовательно, \(S = \pi \cdot 40^2 = 1600\pi\) дм².
Решение задачи состоит из нескольких шагов.
Первым шагом определяем форму сечения шара плоскостью. Известно, что любое сечение шара плоскостью является кругом.
Вторым шагом устанавливаем связь между радиусом шара, расстоянием от центра шара до секущей плоскости и радиусом полученного сечения. Если провести радиус шара к любой точке на окружности сечения, расстояние от центра шара до плоскости сечения и радиус сечения, то получим прямоугольный треугольник. В этом треугольнике радиус шара \(R\) является гипотенузой, а расстояние от центра шара до плоскости \(OB\) и радиус сечения \(AB\) являются катетами. Это соотношение описывается теоремой Пифагора: \(R^2 = OB^2 + AB^2\).
Третьим шагом выражаем радиус сечения \(AB\) из теоремы Пифагора: \(AB^2 = R^2 — OB^2\), следовательно, \(AB = \sqrt{R^2 — OB^2}\).
Четвертым шагом подставляем известные значения радиуса шара \(R = 41\) дм и расстояния от центра до плоскости \(OB = 9\) дм в полученную формулу для нахождения радиуса сечения: \(AB = \sqrt{41^2 — 9^2}\).
Пятым шагом вычисляем значения квадратов и разность под корнем: \(41^2 = 1681\), \(9^2 = 81\). Тогда \(AB = \sqrt{1681 — 81} = \sqrt{1600}\).
Шестым шагом извлекаем квадратный корень: \(AB = 40\) дм. Таким образом, радиус сечения равен 40 дм.
Седьмым шагом находим площадь полученного сечения. Поскольку сечение является кругом с радиусом \(AB\), его площадь \(S\) вычисляется по формуле площади круга: \(S = \pi \cdot AB^2\).
Восьмым шагом подставляем найденное значение радиуса сечения \(AB = 40\) дм в формулу площади: \(S = \pi \cdot 40^2\).
Девятым шагом вычисляем квадрат радиуса сечения и умножаем на \(\pi\): \(40^2 = 1600\). Следовательно, площадь сечения \(S = 1600\pi\) дм².
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.