
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 374 Атанасян — Подробные Ответы
Точки А и В лежат на сфере радиуса R. Найдите расстояние от центра сферы до прямой АВ, если \(АВ = m\).
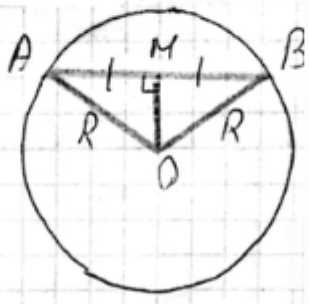
Проведем сечение сферы плоскостью, проходящей через центр О и хорду АВ. В сечении получим окружность радиуса R с центром О. Треугольник АОВ равнобедренный с ОА = ОВ = R. ОМ — расстояние от центра сферы до хорды АВ. В равнобедренном треугольнике АОВ медиана ОМ, проведенная к основанию АВ, является также высотой, поэтому ОМ перпендикулярно АВ, и точка М является серединой отрезка АВ. Следовательно, \(AM = MB = \frac{AB}{2} = \frac{m}{2}\).
Рассмотрим прямоугольный треугольник АОМ с прямым углом при вершине М. По теореме Пифагора имеем \(OA^2 = OM^2 + AM^2\). Подставляя известные значения, получаем \(R^2 = OM^2 + \left(\frac{m}{2}\right)^2\).
Выразим ОМ из этого уравнения: \(OM^2 = R^2 — \left(\frac{m}{2}\right)^2 = R^2 — \frac{m^2}{4}\).
Извлекая квадратный корень, находим ОМ: \(OM = \sqrt{R^2 — \frac{m^2}{4}}\).
Для дальнейшего упрощения приведем подкоренное выражение к общему знаменателю: \(OM = \sqrt{\frac{4R^2}{4} — \frac{m^2}{4}} = \sqrt{\frac{4R^2 — m^2}{4}}\).
Извлекая корень из знаменателя, получаем окончательное выражение для ОМ: \(OM = \frac{\sqrt{4R^2 — m^2}}{2}\).
Рассмотрим сферу с центром в точке О и радиусом R. На поверхности сферы лежат две точки А и В, образующие хорду АВ длиной m. Необходимо найти расстояние от центра сферы О до хорды АВ.
Проведем плоскость через центр сферы О и хорду АВ. Пересечением сферы с этой плоскостью является окружность радиуса R с центром в точке О, проходящая через точки А и В. Таким образом, задача сводится к нахождению расстояния от центра окружности до ее хорды АВ.
Пусть М будет серединой хорды АВ. Расстояние от центра О до хорды АВ — это длина перпендикуляра, опущенного из точки О на прямую АВ. В треугольнике АОВ стороны ОА и ОВ являются радиусами сферы, поэтому \(ОА = ОВ = R\). Треугольник АОВ является равнобедренным с основанием АВ. Отрезок ОМ, соединяющий вершину О с серединой основания М, является медианой равнобедренного треугольника. В равнобедренном треугольнике медиана, проведенная к основанию, также является высотой. Следовательно, ОМ перпендикулярно АВ, и длина отрезка ОМ является искомым расстоянием от центра О до хорды АВ.
Поскольку М является серединой отрезка АВ, длина отрезка АМ равна половине длины отрезка АВ. Дано, что \(АВ = m\), поэтому \(АМ = \frac{m}{2}\).
Теперь рассмотрим прямоугольный треугольник АОМ. Угол при вершине М является прямым, так как ОМ перпендикулярно АВ. Гипотенузой в этом треугольнике является отрезок ОА (радиус сферы), а катетами — отрезки ОМ и АМ. По теореме Пифагора квадрат длины гипотенузы равен сумме квадратов длин катетов: \(OA^2 = OM^2 + AM^2\).
Подставим известные значения в уравнение Пифагора. \(ОА = R\) и \(АМ = \frac{m}{2}\). Получаем: \(R^2 = OM^2 + \left(\frac{m}{2}\right)^2\).
Возведем в квадрат выражение в скобках: \(R^2 = OM^2 + \frac{m^2}{4}\).
Теперь выразим \(OM^2\) из этого уравнения, вычитая \(\frac{m^2}{4}\) из обеих частей: \(OM^2 = R^2 — \frac{m^2}{4}\).
Чтобы найти ОМ, необходимо извлечь квадратный корень из обеих частей уравнения: \(OM = \sqrt{R^2 — \frac{m^2}{4}}\).
Для того чтобы привести выражение под корнем к более удобному виду, приведем дроби к общему знаменателю. Общий знаменатель для \(R^2\) (которое можно представить как \(\frac{R^2}{1}\)) и \(\frac{m^2}{4}\) равен 4. Умножим числитель и знаменатель \(\frac{R^2}{1}\) на 4: \(\frac{4R^2}{4}\).
Таким образом, подкоренное выражение становится: \(R^2 — \frac{m^2}{4} = \frac{4R^2}{4} — \frac{m^2}{4} = \frac{4R^2 — m^2}{4}\).
Теперь подставим это выражение обратно под знак корня: \(OM = \sqrt{\frac{4R^2 — m^2}{4}}\).
Используя свойство корня \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\), разделим корень на числитель и знаменатель: \(OM = \frac{\sqrt{4R^2 — m^2}}{\sqrt{4}}\).
Извлекая квадратный корень из знаменателя \(\sqrt{4} = 2\), получаем окончательное выражение для расстояния ОМ: \(OM = \frac{\sqrt{4R^2 — m^2}}{2}\).
Таким образом, расстояние от центра сферы до хорды АВ равно \(\frac{\sqrt{4R^2 — m^2}}{2}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!