
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 373 Атанасян — Подробные Ответы
Точка М — середина отрезка АВ, концы которого лежат на сфере радиуса R с центром О. Найдите: а) ОМ, если \(R = 50\) см, \(АВ = 40\) см; б) ОМ, если \(R = 15\) мм, \(АВ = 18\) мм; в) АВ, если \(R = 10\) дм, \(ОМ = 60\) см; г) АМ, если \(R = a\), \(OM = b\).
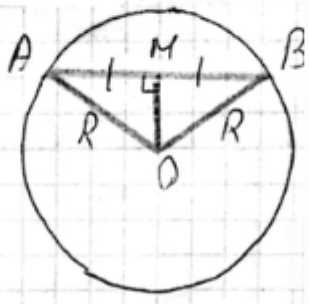
В сечении сферы плоскостью, проходящей через центр О и хорду АВ, образуется окружность радиуса R с центром в точке О. ОМ — медиана в равнобедренном треугольнике АОВ, поэтому ОМ перпендикулярно АВ. Из прямоугольного треугольника АОМ по теореме Пифагора \(OA^2 = OM^2 + AM^2\), или \(R^2 = OM^2 + AM^2\). Также \(AM = \frac{1}{2} AB\).
а) Найти ОМ, если \(R = 50\) см, \(АВ = 40\) см. \(AM = \frac{1}{2} AB = \frac{1}{2} \times 40 = 20\) см. \(OM = \sqrt{R^2 — AM^2} = \sqrt{50^2 — 20^2} = \sqrt{2500 — 400} = \sqrt{2100} = 10\sqrt{21}\) см.
б) Найти ОМ, если \(R = 15\) мм, \(АВ = 18\) мм. \(AM = \frac{1}{2} AB = \frac{1}{2} \times 18 = 9\) мм. \(OM = \sqrt{R^2 — AM^2} = \sqrt{15^2 — 9^2} = \sqrt{225 — 81} = \sqrt{144} = 12\) мм.
в) Найти АВ, если \(R = 10\) дм, \(ОМ = 60\) см. Переведем ОМ в дм: \(ОМ = 60\) см = 6 дм. \(AM = \sqrt{R^2 — OM^2} = \sqrt{10^2 — 6^2} = \sqrt{100 — 36} = \sqrt{64} = 8\) дм. \(AB = 2 \times AM = 2 \times 8 = 16\) дм.
г) Найти АМ, если \(R = a\), \(OM = b\). \(AM = \sqrt{R^2 — OM^2} = \sqrt{a^2 — b^2}\).
Проведем сечение сферы плоскостью, проходящей через центр О и хорду АВ. В этом сечении образуется окружность радиуса R с центром в точке О. Точка М является серединой хорды АВ. В равнобедренном треугольнике АОВ (так как ОА = ОВ = R), ОМ является медианой, проведенной к основанию АВ. Медиана в равнобедренном треугольнике, проведенная к основанию, также является высотой, поэтому ОМ перпендикулярно АВ. Таким образом, треугольник АОМ является прямоугольным с прямым углом при вершине М. По теореме Пифагора в прямоугольном треугольнике АОМ имеем соотношение \(OA^2 = OM^2 + AM^2\). Поскольку ОА является радиусом сферы, \(OA = R\). Следовательно, \(R^2 = OM^2 + AM^2\). Также, поскольку М — середина АВ, длина отрезка АМ равна половине длины отрезка АВ, то есть \(AM = \frac{1}{2} AB\).
а) Дано: \(R = 50\) см, \(АВ = 40\) см. Найти ОМ.
Сначала найдем длину отрезка АМ. Поскольку М — середина АВ, \(AM = \frac{1}{2} AB = \frac{1}{2} \times 40\) см \( = 20\) см.
Теперь, используя теорему Пифагора в треугольнике АОМ, выразим ОМ: \(OM^2 = R^2 — AM^2\).
Подставляем известные значения: \(OM^2 = 50^2 — 20^2 = 2500 — 400 = 2100\).
Извлекаем квадратный корень, чтобы найти ОМ: \(OM = \sqrt{2100} = \sqrt{100 \times 21} = 10\sqrt{21}\) см.
б) Дано: \(R = 15\) мм, \(АВ = 18\) мм. Найти ОМ.
Сначала найдем длину отрезка АМ. Поскольку М — середина АВ, \(AM = \frac{1}{2} AB = \frac{1}{2} \times 18\) мм \( = 9\) мм.
Теперь, используя теорему Пифагора в треугольнике АОМ, выразим ОМ: \(OM^2 = R^2 — AM^2\).
Подставляем известные значения: \(OM^2 = 15^2 — 9^2 = 225 — 81 = 144\).
Извлекаем квадратный корень, чтобы найти ОМ: \(OM = \sqrt{144} = 12\) мм.
в) Дано: \(R = 10\) дм, \(ОМ = 60\) см. Найти АВ.
Прежде всего, приведем все длины к одной единице измерения. Переведем ОМ из сантиметров в дециметры. Поскольку в 1 дм содержится 10 см, \(ОМ = 60\) см \( = \frac{60}{10}\) дм \( = 6\) дм.
Теперь, используя теорему Пифагора в треугольнике АОМ, выразим АМ: \(AM^2 = R^2 — OM^2\).
Подставляем известные значения: \(AM^2 = 10^2 — 6^2 = 100 — 36 = 64\).
Извлекаем квадратный корень, чтобы найти АМ: \(AM = \sqrt{64} = 8\) дм.
Поскольку М — середина АВ, длина отрезка АВ в два раза больше длины отрезка АМ: \(AB = 2 \times AM = 2 \times 8\) дм \( = 16\) дм.
г) Дано: \(R = a\), \(OM = b\). Найти АМ.
Используя теорему Пифагора в треугольнике АОМ, выразим АМ: \(AM^2 = R^2 — OM^2\).
Подставляем данные значения \(R = a\) и \(OM = b\): \(AM^2 = a^2 — b^2\).
Извлекаем квадратный корень, чтобы найти АМ: \(AM = \sqrt{a^2 — b^2}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!