
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 372 Атанасян — Подробные Ответы
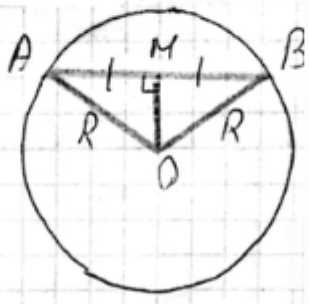
Точки А и В лежат на сфере с центром О и AB, а точка М лежит на отрезке АВ. Докажите, что: а) если М — середина отрезка АВ, то \(OM \perp AB\); б) если \(OM \perp AB\), то М — середина отрезка АВ.
Доказательство:
а) Проведем радиусы \(OA\) и \(OB\). Треугольник \(AOB\) равнобедренный, так как \(OA = OB = R\) (радиусы сферы). Если М — середина отрезка АВ, то ОМ — медиана в равнобедренном треугольнике \(AOB\), проведенная к основанию. Медиана в равнобедренном треугольнике, проведенная к основанию, является также высотой. Следовательно, \(OM \perp AB\).
б) Если \(OM \perp AB\), то треугольники \(OMA\) и \(OMB\) прямоугольные с общим катетом ОМ. Гипотенузы \(OA\) и \(OB\) равны как радиусы сферы (\(OA = OB = R\)). По признаку равенства прямоугольных треугольников по катету и гипотенузе (\(OM\) — общий катет, \(OA = OB\)), треугольник \(OMA\) равен треугольнику \(OMB\). Из равенства треугольников следует равенство соответствующих сторон, то есть \(MA = MB\). Следовательно, точка М — середина отрезка АВ.
Доказательство:
Дано: Точки А и В лежат на сфере с центром О. О не лежит на прямой АВ. Точка М лежит на отрезке АВ.
Требуется доказать, что:
а) Если М — середина отрезка АВ, то \(OM \perp AB\).
б) Если \(OM \perp AB\), то М — середина отрезка АВ.
Доказательство:
а) Рассмотрим треугольник АОВ. Поскольку точки А и В лежат на сфере с центром О, расстояния от центра сферы до этих точек равны радиусу сферы. Следовательно, \(OA = OB = R\), где \(R\) — радиус сферы. Таким образом, треугольник АОВ является равнобедренным с основанием АВ. По условию, М является серединой отрезка АВ. Это означает, что отрезок ОМ является медианой треугольника АОВ, проведенной из вершины О к основанию АВ. В равнобедренном треугольнике медиана, проведенная к основанию, одновременно является и высотой. Следовательно, отрезок ОМ перпендикулярен основанию АВ, то есть \(OM \perp AB\).
б) Рассмотрим треугольник АОВ. Мы уже установили, что он равнобедренный с \(OA = OB = R\). По условию, \(OM \perp AB\). Это означает, что отрезок ОМ является высотой треугольника АОВ, проведенной из вершины О к стороне АВ. Рассмотрим два прямоугольных треугольника ОМА и ОМВ. Оба эти треугольника являются прямоугольными, так как ОМ перпендикулярен АВ в точке М. Отрезок ОМ является общим катетом для обоих треугольников ОМА и ОМВ. Гипотенузы этих прямоугольных треугольников — это отрезки ОА и ОВ, которые равны как радиусы сферы (\(OA = OB = R\)). По признаку равенства прямоугольных треугольников по катету и гипотенузе (общий катет ОМ и равные гипотенузы ОА и ОВ), треугольник ОМА равен треугольнику ОМВ. Из равенства треугольников следует равенство их соответствующих сторон. В частности, стороны МА и МВ, лежащие напротив общего катета ОМ, равны. Таким образом, \(MA = MB\). Поскольку точка М лежит на отрезке АВ и делит его на два равных отрезка МА и МВ, М является серединой отрезка АВ.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!