
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 371 Атанасян — Подробные Ответы
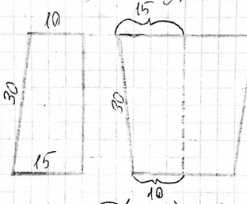
Ведро имеет форму усечённого конуса, радиусы оснований которого равны 15 см и 10 см, а образующая равна 30 см. Сколько килограммов краски нужно взять для того, чтобы покрасить с обеих сторон 100 таких вёдер, если на 1 м\(^2\) требуется 150 г краски? (Толщину стенок вёдер в расчёт не принимать.
Дано: \(L = 30\) см, \(r_1 = 15\) см, \(r_2 = 10\) см. Расход краски: \(150\) г на \(1\) м\(^2\). Количество ведер: \(N = 100\).
Решение:
Площадь боковой поверхности усеченного конуса равна \(S_{бок} = \pi (r_1 + r_2) L\). Площадь малого основания равна \(S_{малое\_осн} = \pi r_2^2\). Согласно представленному решению, площадь для покраски одного ведра с обеих сторон составляет \(S_{ведро} = 2 \times (S_{бок} + S_{малое\_осн})\).
Подставляя значения, получаем \(S_{ведро} = 2 \times (\pi (15 + 10) \cdot 30 + \pi \cdot 10^2) =\)
\(= 2 \times (\pi \cdot 25 \cdot 30 + \pi \cdot 100) = 2 \times (750\pi + 100\pi) = 2 \times 850\pi = 1700\pi\) см\(^2\).
Переводя в квадратные метры, учитывая, что \(1\) м\(^2\) = \(10000\) см\(^2\), получаем \(S_{ведро} = \frac{1700\pi}{10000} = 0.17\pi\) м\(^2\).
Общая площадь для покраски \(100\) ведер составляет \(S_{общая} = 100 \times S_{ведро} = 100 \times 0.17\pi = 17\pi\) м\(^2\).
Расход краски \(150\) г на \(1\) м\(^2\) эквивалентен \(0.15\) кг на \(1\) м\(^2\).
Общее количество краски в килограммах равно \(17\pi \times 0.15 = 2.55\pi\) кг.
Приближенное значение составляет около \(8\) кг.
Ответ: \(2.55\pi\) кг \(\approx 8\) кг.
Даны размеры ведра: образующая \(L = 30\) см, радиус большего основания \(r_1 = 15\) см, радиус меньшего основания \(r_2 = 10\) см. Ведро имеет форму усеченного конуса. Красить нужно с обеих сторон. Расход краски составляет \(150\) г на \(1\) м\(^2\). Необходимо покрасить \(100\) таких ведер.
Сначала найдем площадь поверхности одного ведра, которую нужно покрасить. Ведро красится с обеих сторон, включая боковую поверхность и дно. Верх ведра открыт. Таким образом, для одной стороны ведра площадь покраски включает площадь боковой поверхности усеченного конуса и площадь его меньшего основания (дна).
Площадь боковой поверхности усеченного конуса вычисляется по формуле \(S_{бок} = \pi (r_1 + r_2) L\). Подставляя данные значения, получаем \(S_{бок} = \pi (15 + 10) \cdot 30 = \pi \cdot 25 \cdot 30 = 750\pi\) см\(^2\).
Площадь меньшего основания (дна) вычисляется по формуле площади круга \(S_{дно} = \pi r_2^2\). Подставляя значение радиуса меньшего основания, получаем \(S_{дно} = \pi \cdot 10^2 = 100\pi\) см\(^2\).
Площадь поверхности одного ведра, которую нужно покрасить с одной стороны, равна сумме площади боковой поверхности и площади дна: \(S_{одна\_сторона} = S_{бок} + S_{дно} = 750\pi + 100\pi = 850\pi\) см\(^2\).
Поскольку ведра нужно покрасить с обеих сторон, общая площадь покраски одного ведра составляет \(S_{ведро} = 2 \times S_{одна\_сторона} = 2 \times 850\pi = 1700\pi\) см\(^2\).
Расход краски дан в граммах на квадратный метр, поэтому необходимо перевести площадь из квадратных сантиметров в квадратные метры. Известно, что \(1\) метр равен \(100\) сантиметрам, следовательно, \(1\) квадратный метр равен \(100 \times 100 = 10000\) квадратных сантиметров.
Площадь одного ведра в квадратных метрах равна \(S_{ведро\_м^2} = \frac{1700\pi}{10000} = 0.17\pi\) м\(^2\).
Теперь вычислим общую площадь покраски для \(100\) ведер. Общая площадь равна произведению количества ведер на площадь покраски одного ведра: \(S_{общая} = 100 \times S_{ведро\_м^2} = 100 \times 0.17\pi = 17\pi\) м\(^2\).
Расход краски составляет \(150\) г на \(1\) м\(^2\). Переведем расход краски в килограммы на квадратный метр, учитывая, что в \(1\) килограмме \(1000\) грамм: \(150\) г = \(\frac{150}{1000}\) кг = \(0.15\) кг. Таким образом, расход краски составляет \(0.15\) кг на \(1\) м\(^2\).
Общее количество краски, необходимое для покраски \(100\) ведер, равно произведению общей площади покраски на расход краски на один квадратный метр: Количество краски = \(S_{общая} \times \text{Расход краски на } 1 \text{ м}^2\).
Количество краски = \(17\pi \times 0.15 = 2.55\pi\) кг.
Для получения приближенного значения, используем приближенное значение числа \(\pi \approx 3.14159\).
Количество краски \(\approx 2.55 \times 3.14159 \approx 8.005\) кг.
Ответ: \(2.55\pi\) кг \(\approx 8\) кг.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!