ГДЗ по Геометрии 10 класс Номер 368 Атанасян — Подробные Ответы

Радиусы оснований усечённого конуса равны R и r, где \(R>r\), а образующая составляет с плоскостью основания угол в \(45^\circ\). Найдите площадь осевого сечения.

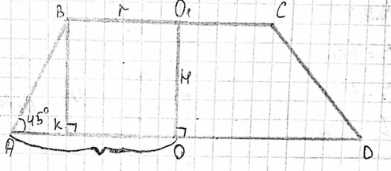
Осевое сечение усеченного конуса является равнобочной трапецией с основаниями, равными диаметрам оснований конуса, то есть \(2r\) и \(2R\). Высота этой трапеции равна высоте усеченного конуса \(H\).
Рассмотрим прямоугольный треугольник, образованный высотой \(H\), образующей конуса и отрезком на большем основании, равным разности радиусов \(R-r\). Угол между образующей и плоскостью основания равен \(45^\circ\). В прямоугольном треугольнике с углом \(45^\circ\) катеты равны. Один катет равен высоте \(H\), другой катет равен разности радиусов \(R-r\). Следовательно, \(H = R-r\).
Площадь осевого сечения \(S_{сеч}\) как площадь трапеции вычисляется по формуле: \(S_{сеч} = \frac{\text{сумма оснований}}{2} \times \text{высота}\).
Подставляем значения оснований \(2r\) и \(2R\), и высоты \(H = R-r\): \(S_{сеч} = \frac{2r + 2R}{2} \times (R-r)\).
Упрощаем выражение: \(S_{сеч} = \frac{2(r + R)}{2} \times (R-r)\).
\(S_{сеч} = (r + R) \times (R-r)\).
Используя формулу разности квадратов \((a+b)(a-b) = a^2 — b^2\), получаем: \(S_{сеч} = R^2 — r^2\).

Осевое сечение усеченного конуса представляет собой равнобочную трапецию. Основания этой трапеции равны диаметрам оснований усеченного конуса. Диаметр меньшего основания равен \(2r\), а диаметр большего основания равен \(2R\). Высота этой трапеции совпадает с высотой усеченного конуса, которую обозначим через \(H\).

Для нахождения высоты \(H\) рассмотрим прямоугольный треугольник, образованный высотой усеченного конуса, его образующей и отрезком на большем основании. Этот отрезок равен разности радиусов оснований, то есть \(R-r\). Образующая усеченного конуса является гипотенузой этого прямоугольного треугольника. По условию задачи, образующая составляет с плоскостью основания угол \(45^\circ\). В данном прямоугольном треугольнике этот угол равен \(45^\circ\).

Так как один из острых углов прямоугольного треугольника равен \(45^\circ\), то второй острый угол также равен \(90^\circ — 45^\circ = 45^\circ\). Следовательно, этот прямоугольный треугольник является равнобедренным, и его катеты равны. Один катет равен высоте \(H\), а другой катет равен разности радиусов \(R-r\). Из равенства катетов следует, что высота усеченного конуса \(H\) равна разности радиусов оснований: \(H = R-r\).

Площадь осевого сечения, являющегося трапецией, вычисляется по формуле площади трапеции: сумма оснований, деленная на два, умноженная на высоту. Основания трапеции равны \(2r\) и \(2R\), а высота равна \(H\).
Таким образом, площадь осевого сечения \(S_{сеч}\) равна: \(S_{сеч} = \frac{(2r + 2R)}{2} \times H\).

Подставим в эту формулу найденное значение высоты \(H = R-r\): \(S_{сеч} = \frac{(2r + 2R)}{2} \times (R-r)\).
Вынесем общий множитель \(2\) в числителе: \(S_{сеч} = \frac{2(r + R)}{2} \times (R-r)\).
Сократим дробь на \(2\): \(S_{сеч} = (r + R) \times (R-r)\).

Применим формулу разности квадратов \((a+b)(a-b) = a^2 — b^2\). В нашем случае \(a=R\) и \(b=r\).
Следовательно, \(S_{сеч} = R^2 — r^2\).

Таким образом, площадь осевого сечения усеченного конуса равна разности квадратов радиусов его оснований.