Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 367 Атанасян — Подробные Ответы
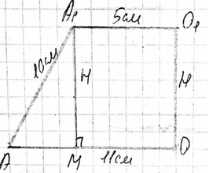
Радиусы оснований усечённого конуса равны 5 см и 11 см, а образующая равна 10 см. Найдите: а) высоту усечённого конуса; б) площадь осевого сечения.
Дано: радиус меньшего основания \(r_1 = 5\) см, радиус большего основания \(r_2 = 11\) см, образующая \(L = 10\) см.
а) Найдем высоту усеченного конуса \(H\). Рассмотрим прямоугольный треугольник, образованный высотой \(H\), образующей \(L\) и разностью радиусов оснований \((r_2 — r_1)\). По теореме Пифагора имеем \(L^2 = H^2 + (r_2 — r_1)^2\).
Разность радиусов \((r_2 — r_1) = 11 — 5 = 6\) см.
Подставляем значения: \(10^2 = H^2 + 6^2\).
\(100 = H^2 + 36\).
\(H^2 = 100 — 36\).
\(H^2 = 64\).
\(H = \sqrt{64} = 8\) см.
б) Найдем площадь осевого сечения \(S_{сеч}\). Осевое сечение усеченного конуса является трапецией. Согласно примеру, площадь вычисляется по формуле \(\frac{r_1 + r_2}{2} \times H\).
Подставляем значения: \(S_{сеч} = \frac{5 + 11}{2} \times 8\).
\(S_{сеч} = \frac{16}{2} \times 8\).
\(S_{сеч} = 8 \times 8 = 64\) см².
Дано: усеченный конус с радиусом меньшего основания \(r_1 = 5\) см, радиусом большего основания \(r_2 = 11\) см и образующей \(L = 10\) см. Требуется найти высоту усеченного конуса \(H\) и площадь его осевого сечения \(S_{сеч}\).
Решение:
а) Нахождение высоты усеченного конуса \(H\).
Рассмотрим осевое сечение усеченного конуса. Это равнобочная трапеция. Опустим высоту из вершины верхнего основания трапеции на нижнее основание. Эта высота равна высоте усеченного конуса \(H\). При этом на нижнем основании отсекается отрезок, равный разности радиусов оснований \(r_2 — r_1\). Образующая усеченного конуса \(L\) является боковой стороной этой трапеции. Таким образом, образуется прямоугольный треугольник, где катеты равны высоте \(H\) и разности радиусов \((r_2 — r_1)\), а гипотенуза равна образующей \(L\).
Разность радиусов оснований равна \(r_2 — r_1 = 11 \text{ см} — 5 \text{ см} = 6\) см.
По теореме Пифагора в этом прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: \(L^2 = H^2 + (r_2 — r_1)^2\).
Подставляем известные значения: \((10 \text{ см})^2 = H^2 + (6 \text{ см})^2\).
\(100 \text{ см}^2 = H^2 + 36 \text{ см}^2\).
Выразим \(H^2\): \(H^2 = 100 \text{ см}^2 — 36 \text{ см}^2\).
\(H^2 = 64 \text{ см}^2\).
Извлекаем квадратный корень для нахождения \(H\): \(H = \sqrt{64 \text{ см}^2}\).
\(H = 8\) см.
б) Нахождение площади осевого сечения \(S_{сеч}\).
Осевое сечение усеченного конуса представляет собой трапецию, параллельные стороны которой равны диаметрам оснований усеченного конуса (\(2r_1\) и \(2r_2\)), а высота равна высоте конуса \(H\). Однако, согласно предоставленному примеру и рисунку, осевое сечение рассматривается как трапеция с параллельными сторонами, равными радиусам оснований (\(r_1\) и \(r_2\)), и высотой \(H\). Площадь трапеции вычисляется по формуле: \(S = \frac{\text{сумма параллельных сторон}}{2} \times \text{высота}\).
В данном случае, принимая параллельные стороны равными радиусам \(r_1\) и \(r_2\), и высоту равной \(H\), площадь осевого сечения будет: \(S_{сеч} = \frac{r_1 + r_2}{2} \times H\).
Подставляем значения \(r_1 = 5\) см, \(r_2 = 11\) см и \(H = 8\) см: \(S_{сеч} = \frac{5 \text{ см} + 11 \text{ см}}{2} \times 8 \text{ см}\).
\(S_{сеч} = \frac{16 \text{ см}}{2} \times 8 \text{ см}\).
\(S_{сеч} = 8 \text{ см} \times 8 \text{ см}\).
\(S_{сеч} = 64\) см².
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.