Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 366 Атанасян — Подробные Ответы
Найдите образующую усечённого конуса, если радиусы оснований равны 3 см и 6 см, а высота равна 4 см.
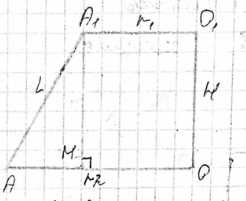
Для нахождения образующей \(L\) усеченного конуса рассмотрим прямоугольный треугольник, образованный высотой конуса \(H\), разностью радиусов оснований \(r_2 — r_1\) и образующей \(L\).
По теореме Пифагора имеем \(L^2 = H^2 + (r_2 — r_1)^2\).
Дано: \(H = 4\) см, \(r_1 = 3\) см, \(r_2 = 6\) см.
Разность радиусов составляет \(r_2 — r_1 = 6 — 3 = 3\) см.
Подставим значения в формулу: \(L^2 = 4^2 + 3^2 = 16 + 9 = 25\).
Следовательно, \(L = \sqrt{25} = 5\) см.
Ответ: \(L = 5\) см.
Для решения данной задачи нам необходимо найти образующую усеченного конуса. У нас есть усеченный конус с высотой \(H\), радиусом меньшего основания \(r_1\) и радиусом большего основания \(r_2\). Образующая усеченного конуса \(L\) — это отрезок, соединяющий соответствующие точки окружностей оснований.
Представим осевое сечение усеченного конуса. Это равнобочная трапеция. Высота трапеции равна высоте конуса \(H\), а основания трапеции равны диаметрам оснований конуса, то есть \(2r_1\) и \(2r_2\). Боковые стороны трапеции являются образующими усеченного конуса \(L\).
Чтобы найти образующую \(L\), мы можем опустить перпендикуляр из вершины верхнего основания трапеции на нижнее основание. Этот перпендикуляр будет равен высоте конуса \(H\). При этом на нижнем основании отсекается отрезок, равный разности радиусов оснований \(r_2 — r_1\). Таким образом, образуется прямоугольный треугольник, в котором одним катетом является высота конуса \(H\), другим катетом — разность радиусов оснований \(r_2 — r_1\), а гипотенузой — образующая усеченного конуса \(L\).
Согласно теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов. Применительно к нашему прямоугольному треугольнику это означает, что \(L^2 = H^2 + (r_2 — r_1)^2\).
В данной задаче нам даны следующие значения:
Высота усеченного конуса \(H = 4\) см.
Радиус меньшего основания \(r_1 = 3\) см.
Радиус большего основания \(r_2 = 6\) см.
Сначала найдем разность радиусов оснований: \(r_2 — r_1 = 6 \text{ см} — 3 \text{ см} = 3\) см.
Теперь подставим известные значения \(H\) и \((r_2 — r_1)\) в формулу теоремы Пифагора для нахождения \(L\):
\(L^2 = (4 \text{ см})^2 + (3 \text{ см})^2\)
\(L^2 = 16 \text{ см}^2 + 9 \text{ см}^2\)
\(L^2 = 25 \text{ см}^2\)
Чтобы найти \(L\), извлечем квадратный корень из обеих частей уравнения:
\(L = \sqrt{25 \text{ см}^2}\)
\(L = 5\) см.
Таким образом, образующая усеченного конуса равна 5 см.
Ответ: \(L = 5\) см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.