Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 365 Атанасян — Подробные Ответы
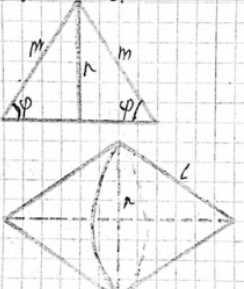
Равнобедренный треугольник, боковая сторона которого равна m, а угол при основании равен \(\phi\), вращается вокруг основания. Найдите площадь поверхности тела, полученного при вращении треугольника.
Радиус основания конуса \(r\) равен высоте равнобедренного треугольника, опущенной на основание. Боковая сторона треугольника \(m\) является образующей конуса \(l\). Угол при основании треугольника \(\phi\).
Тогда \(r = m \sin\phi\) и \(l = m\).
Площадь боковой поверхности одного конуса \(S_{\text{бок}} = \pi r l = \pi (m \sin\phi) m = \pi m^2 \sin\phi\).
Тело вращения состоит из двух таких конусов, поэтому полная площадь поверхности тела вращения \(S_{\text{пов}} = 2 S_{\text{бок}} = 2 \pi m^2 \sin\phi\).
Рассмотрим равнобедренный треугольник с боковой стороной \(m\) и углом при основании \(\phi\). Когда этот треугольник вращается вокруг своего основания, образуется тело вращения, состоящее из двух одинаковых конусов, соединенных своими основаниями.
Основание равнобедренного треугольника становится осью вращения. Высота равнобедренного треугольника, опущенная на основание, становится радиусом основания каждого из конусов. Боковая сторона равнобедренного треугольника становится образующей каждого из конусов.
Найдем радиус основания конуса, который обозначим как \(r\). В равнобедренном треугольнике высота к основанию делит его на два равных прямоугольных треугольника. В таком прямоугольном треугольнике гипотенуза равна боковой стороне исходного равнобедренного треугольника, то есть \(m\). Угол при основании исходного треугольника \(\phi\) является одним из острых углов этого прямоугольного треугольника. Высота, которая является радиусом основания конуса \(r\), находится напротив угла \(\phi\). Следовательно, используя определение синуса в прямоугольном треугольнике (\(\sin(\text{угол}) = \frac{\text{противолежащий катет}}{\text{гипотенуза}}\)), получаем \(r = m \sin\phi\).
Образующая конуса \(l\) равна боковой стороне исходного равнобедренного треугольника, то есть \(l = m\).
Площадь боковой поверхности одного конуса вычисляется по формуле \(S_{\text{бок}} = \pi r l\). Подставим найденные значения \(r\) и \(l\) в эту формулу: \(S_{\text{бок}} = \pi (m \sin\phi) m = \pi m^2 \sin\phi\).
Тело вращения состоит из двух таких конусов, соединенных по их основаниям. Площадь поверхности тела вращения включает только боковые поверхности этих двух конусов, так как их основания находятся внутри тела и не являются частью внешней поверхности. Поэтому полная площадь поверхности тела вращения \(S_{\text{пов}}\) равна удвоенной площади боковой поверхности одного конуса: \(S_{\text{пов}} = 2 \times S_{\text{бок}}\).
Подставим значение \(S_{\text{бок}}\): \(S_{\text{пов}} = 2 (\pi m^2 \sin\phi) = 2 \pi m^2 \sin\phi\).
Таким образом, площадь поверхности тела, полученного при вращении равнобедренного треугольника вокруг основания, равна \(2 \pi m^2 \sin\phi\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.