Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 364 Атанасян — Подробные Ответы
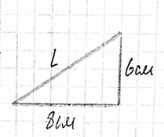
Прямоугольный треугольник с катетами 6 см и 8 см вращается вокруг меньшего катета. Вычислите площади боковой и полной поверхностей образованного при этом вращении конуса
При вращении прямоугольного треугольника с катетами 6 см и 8 см вокруг меньшего катета образуется конус. Высота этого конуса равна меньшему катету, то есть \(h = 6\) см, а радиус основания равен большему катету, то есть \(R = 8\) см. Образующая конуса \(L\) является гипотенузой этого прямоугольного треугольника.
Найдем образующую \(L\) по теореме Пифагора: \(L = \sqrt{R^2 + h^2} = \sqrt{8^2 + 6^2} = \sqrt{64 + 36} = \sqrt{100} = 10\) см.
Площадь боковой поверхности конуса вычисляется по формуле \(S_{\text{бок}} = \pi R L\). Подставим значения \(R = 8\) см и \(L = 10\) см: \(S_{\text{бок}} = \pi \cdot 8 \cdot 10 = 80\pi\) см².
Площадь полной поверхности конуса вычисляется по формуле \(S_{\text{полн}} = \pi R (R + L)\). Подставим значения \(R = 8\) см и \(L = 10\) см: \(S_{\text{полн}} = \pi \cdot 8 (8 + 10) = \pi \cdot 8 \cdot 18 = 144\pi\) см².
При вращении прямоугольного треугольника вокруг одного из его катетов образуется геометрическое тело, называемое конусом. В данном случае прямоугольный треугольник имеет катеты длиной 6 см и 8 см. По условию, вращение происходит вокруг меньшего катета, длина которого составляет 6 см.
При таком вращении:
Меньший катет треугольника становится высотой конуса, поэтому высота конуса \(h = 6\) см.
Больший катет треугольника становится радиусом основания конуса, поэтому радиус основания конуса \(R = 8\) см.
Гипотенуза прямоугольного треугольника становится образующей конуса, обозначаемой \(L\).
Для того чтобы найти площадь боковой и полной поверхностей конуса, нам необходимо знать длину образующей \(L\). Образующая \(L\), радиус основания \(R\) и высота \(h\) связаны соотношением прямоугольного треугольника (по теореме Пифагора), где \(L\) является гипотенузой, а \(R\) и \(h\) — катетами. Следовательно, \(L^2 = R^2 + h^2\). Подставляя известные значения \(R = 8\) см и \(h = 6\) см, получаем:
\(L^2 = 8^2 + 6^2\)
\(L^2 = 64 + 36\)
\(L^2 = 100\)
Извлекая квадратный корень из обеих частей уравнения, находим длину образующей:
\(L = \sqrt{100} = 10\) см.
Теперь, когда известны радиус основания \(R\) и образующая \(L\), мы можем вычислить площади боковой и полной поверхностей конуса.
Площадь боковой поверхности конуса \(S_{\text{бок}}\) вычисляется по формуле:
\(S_{\text{бок}} = \pi R L\)
Подставляем значения \(R = 8\) см и \(L = 10\) см:
\(S_{\text{бок}} = \pi \cdot 8 \cdot 10\)
\(S_{\text{бок}} = 80\pi\) см².
Площадь полной поверхности конуса \(S_{\text{полн}}\) состоит из площади боковой поверхности и площади основания. Площадь основания конуса, которое является кругом, вычисляется по формуле \(S_{\text{осн}} = \pi R^2\). Таким образом, площадь полной поверхности конуса \(S_{\text{полн}}\) вычисляется по формуле:
\(S_{\text{полн}} = S_{\text{бок}} + S_{\text{осн}}\)
\(S_{\text{полн}} = \pi R L + \pi R^2\)
Эту формулу также можно записать в виде:
\(S_{\text{полн}} = \pi R (L + R)\)
Подставляем значения \(R = 8\) см и \(L = 10\) см:
\(S_{\text{полн}} = \pi \cdot 8 (10 + 8)\)
\(S_{\text{полн}} = \pi \cdot 8 \cdot 18\)
\(S_{\text{полн}} = 144\pi\) см².
Таким образом, площадь боковой поверхности образованного конуса равна \(80\pi\) см², а площадь полной поверхности равна \(144\pi\) см².
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.