ГДЗ по Геометрии 10 класс Номер 363 Атанасян — Подробные Ответы

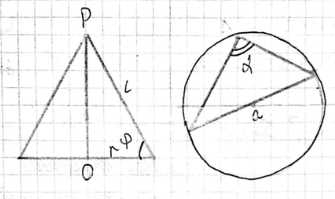
Образующая конуса наклонена к плоскости основания под углом \(\phi\). В основание конуса вписан треугольник, у которого одна сторона равна а, а противолежащий угол равен \(\alpha\). Найдите площадь полной поверхности конуса.

По теореме синусов радиус основания конуса \(R = \frac{a}{2 \sin \alpha}\). Образующая конуса \(L\) связана с радиусом основания и углом \(\phi\) соотношением \(L = \frac{R}{\cos \phi}\). Подставляя выражение для \(R\), получаем \(L = \frac{a}{2 \sin \alpha \cos \phi}\). Площадь полной поверхности конуса равна сумме площади основания и площади боковой поверхности: \(S_{\text{полн}} = \pi R^2 + \pi RL = \pi R(R+L)\). Подставляя выражения для \(R\) и \(L\), находим \(S_{\text{полн}} = \pi \frac{a}{2 \sin \alpha} \left(\frac{a}{2 \sin \alpha} + \frac{a}{2 \sin \alpha \cos \phi}\right) = \frac{\pi a^2}{4 \sin^2 \alpha} \left(1 + \frac{1}{\cos \phi}\right) = \frac{\pi a^2 (1 + \cos \phi)}{4 \sin^2 \alpha \cos \phi}\).

Решение задачи начинается с определения формулы площади полной поверхности конуса. Площадь полной поверхности конуса \(S_{\text{полн}}\) состоит из площади основания \(S_{\text{осн}}\) и площади боковой поверхности \(S_{\text{бок}}\). Площадь основания, являющегося кругом радиуса \(R\), равна \(S_{\text{осн}} = \pi R^2\). Площадь боковой поверхности конуса с радиусом основания \(R\) и образующей \(L\) равна \(S_{\text{бок}} = \pi R L\). Таким образом, площадь полной поверхности конуса выражается формулой \(S_{\text{полн}} = \pi R^2 + \pi R L = \pi R (R+L)\). Для нахождения площади полной поверхности конуса необходимо определить радиус основания \(R\) и образующую \(L\) через заданные в условии величины \(a\), \(\alpha\) и \(\phi\).

В основание конуса вписан треугольник. Одна сторона этого треугольника равна \(a\), а противолежащий ей угол равен \(\alpha\). Поскольку треугольник вписан в основание конуса, окружность основания конуса является описанной окружностью для этого треугольника. По теореме синусов для любого треугольника отношение длины стороны к синусу противолежащего угла равно удвоенному радиусу описанной окружности. В данном случае, для стороны \(a\) и противолежащего угла \(\alpha\), мы имеем \(\frac{a}{\sin \alpha} = 2R\), где \(R\) — радиус описанной окружности, то есть радиус основания конуса. Из этого соотношения выразим радиус основания \(R\): \(R = \frac{a}{2 \sin \alpha}\).

Далее необходимо найти образующую конуса \(L\). По условию образующая конуса наклонена к плоскости основания под углом \(\phi\). Рассмотрим прямоугольный треугольник, образованный высотой конуса \(h\), радиусом основания \(R\) и образующей \(L\). В этом треугольнике радиус основания \(R\) является катетом, прилежащим к углу \(\phi\), а образующая \(L\) является гипотенузой. Связь между этими элементами выражается через косинус угла \(\phi\): \(\cos \phi = \frac{R}{L}\). Из этого уравнения выразим образующую \(L\): \(L = \frac{R}{\cos \phi}\).

Теперь подставим найденное выражение для радиуса основания \(R\) в формулу для образующей \(L\): \(L = \frac{\frac{a}{2 \sin \alpha}}{\cos \phi} = \frac{a}{2 \sin \alpha \cos \phi}\).

Теперь у нас есть выражения для радиуса основания \(R\) и образующей \(L\) через заданные величины \(a\), \(\alpha\) и \(\phi\). Подставим эти выражения в формулу площади полной поверхности конуса \(S_{\text{полн}} = \pi R (R+L)\):
\(S_{\text{полн}} = \pi \left(\frac{a}{2 \sin \alpha}\right) \left(\frac{a}{2 \sin \alpha} + \frac{a}{2 \sin \alpha \cos \phi}\right)\).

Вынесем общий множитель \(\frac{a}{2 \sin \alpha}\) из скобок:
\(S_{\text{полн}} = \pi \frac{a}{2 \sin \alpha} \cdot \frac{a}{2 \sin \alpha} \left(1 + \frac{1}{\cos \phi}\right)\).
Упростим выражение:
\(S_{\text{полн}} = \frac{\pi a^2}{4 \sin^2 \alpha} \left(1 + \frac{1}{\cos \phi}\right)\).

Для дальнейшего упрощения приведем выражение в скобках к общему знаменателю:
\(1 + \frac{1}{\cos \phi} = \frac{\cos \phi}{\cos \phi} + \frac{1}{\cos \phi} = \frac{\cos \phi + 1}{\cos \phi}\).
Подставим это обратно в выражение для \(S_{\text{полн}}\):
\(S_{\text{полн}} = \frac{\pi a^2}{4 \sin^2 \alpha} \left(\frac{1 + \cos \phi}{\cos \phi}\right)\).
Окончательно получаем формулу для площади полной поверхности конуса:
\(S_{\text{полн}} = \frac{\pi a^2 (1 + \cos \phi)}{4 \sin^2 \alpha \cos \phi}\).