
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 362 Атанасян — Подробные Ответы
Площадь осевого сечения конуса равна 0,6 см\(^2\). Высота конуса равна 1,2 см. Вычислите площадь полной поверхности конуса
Площадь осевого сечения конуса равна \(S_{сеч} = r \cdot H\). Подставляя известные значения, получаем \(0.6 = r \cdot 1.2\), откуда радиус основания конуса \(r = \frac{0.6}{1.2} = 0.5\) см. Образующая конуса \(L\) находится по формуле Пифагора \(L = \sqrt{H^2 + r^2} = \sqrt{1.2^2 + 0.5^2} = \sqrt{1.44 + 0.25} = \sqrt{1.69} = 1.3\) см. Площадь полной поверхности конуса вычисляется по формуле \(S_{полн} = \pi r (L + r)\). Подставляем значения \(S_{полн} = \pi \cdot 0.5 \cdot (1.3 + 0.5) = \pi \cdot 0.5 \cdot 1.8 = 0.9\pi\) см\(^2\). Ответ: \(0.9\pi\) см\(^2\).
Дано: площадь осевого сечения конуса \(S_{сеч} = 0.6\) см\(^2\), высота конуса \(H = 1.2\) см. Найти: площадь полной поверхности конуса \(S_{полн}\).
Решение:
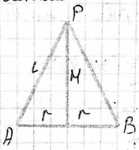
Осевое сечение конуса представляет собой равнобедренный треугольник, основанием которого является диаметр основания конуса \(2r\), а высотой — высота конуса \(H\). Площадь треугольника вычисляется по формуле \(S = \frac{1}{2} \cdot основание \cdot высота\). В данном случае, площадь осевого сечения \(S_{сеч} = \frac{1}{2} \cdot (2r) \cdot H = r \cdot H\).
Нам известны \(S_{сеч}\) и \(H\), поэтому мы можем найти радиус основания конуса \(r\). Подставляем данные значения в формулу: \(0.6 = r \cdot 1.2\).
Чтобы найти \(r\), разделим обе части уравнения на \(1.2\): \(r = \frac{0.6}{1.2}\).
Выполняем деление: \(r = \frac{6}{12} = \frac{1}{2} = 0.5\) см.
Теперь нам нужно найти образующую конуса \(L\). Образующая, высота и радиус основания конуса образуют прямоугольный треугольник, где образующая является гипотенузой, а высота и радиус — катетами. По теореме Пифагора \(L^2 = H^2 + r^2\).
Подставляем известные значения \(H = 1.2\) и \(r = 0.5\): \(L^2 = (1.2)^2 + (0.5)^2\).
Вычисляем квадраты: \(L^2 = 1.44 + 0.25\).
Складываем значения: \(L^2 = 1.69\).
Чтобы найти \(L\), извлекаем квадратный корень: \(L = \sqrt{1.69}\).
\(L = 1.3\) см.
Площадь полной поверхности конуса \(S_{полн}\) состоит из площади основания \(S_{осн}\) и площади боковой поверхности \(S_{бок}\). Площадь основания — это площадь круга с радиусом \(r\), которая вычисляется по формуле \(S_{осн} = \pi r^2\). Площадь боковой поверхности вычисляется по формуле \(S_{бок} = \pi r L\). Таким образом, площадь полной поверхности конуса \(S_{полн} = S_{осн} + S_{бок} = \pi r^2 + \pi r L = \pi r (r + L)\).
Подставляем найденные значения \(r = 0.5\) и \(L = 1.3\) в формулу площади полной поверхности: \(S_{полн} = \pi \cdot 0.5 \cdot (0.5 + 1.3)\).
Складываем значения в скобках: \(S_{полн} = \pi \cdot 0.5 \cdot 1.8\).
Умножаем значения: \(S_{полн} = 0.9\pi\) см\(^2\).
Ответ: площадь полной поверхности конуса равна \(0.9\pi\) см\(^2\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!