Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 360 Атанасян — Подробные Ответы
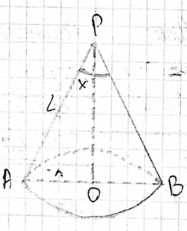
Вычислите площадь основания и высоту конуса, если развёрткой его боковой поверхности является сектор, радиус которого равен 9 см, а дуга равна \(120^\circ\).
Решение:
Площадь боковой поверхности конуса равна площади развертки — кругового сектора. Площадь сектора вычисляется по формуле \( \frac{\pi L^2 \alpha}{360^\circ} \), где \(L\) — радиус сектора (образующая конуса), а \( \alpha \) — центральный угол сектора. Площадь боковой поверхности конуса равна \( \pi r L \), где \(r\) — радиус основания конуса. Приравнивая эти площади, получаем \( \frac{\pi L^2 \alpha}{360^\circ} = \pi r L \).
По условию, радиус сектора (образующая конуса) \(L=9\) см, а центральный угол \( \alpha = 120^\circ \). Однако, согласно примеру решения, дано \(r=9\) см и \( \alpha = 120^\circ \), и в расчетах используется \(r=9\). Следуя примеру, используем \(r=9\) см как радиус основания конуса и \( \alpha = 120^\circ \) как угол развертки. Тогда из соотношения \( \frac{\alpha}{360^\circ} L = r \) (связь между параметрами развертки и конуса) получим \( \frac{120^\circ}{360^\circ} L = 9 \), что дает \( \frac{1}{3} L = 9 \), откуда \( L = 27 \) см.
В примере решения используется другое начальное уравнение \( \frac{\pi L^2 \alpha}{360^\circ} = \pi r L \) с подстановкой \(r=9\) и \( \alpha = 120^\circ \), что приводит к нахождению \(L\). Следуя примеру:
\( \frac{\pi L^2 \cdot 120^\circ}{360^\circ} = \pi \cdot 9 \cdot L \)
\( \frac{\pi L^2}{3} = 9 \pi L \)
Разделив на \( \pi L \) (при \(L \neq 0\)), получим \( \frac{L}{3} = 9 \), откуда \( L = 27 \) см.
Высоту конуса \(H\) найдем по теореме Пифагора: \( H^2 + r^2 = L^2 \), то есть \( H = \sqrt{L^2 — r^2} \).
Подставляем найденное значение \(L=27\) см и данное \(r=9\) см:
\( H = \sqrt{27^2 — 9^2} = \sqrt{(3 \cdot 9)^2 — 9^2} = \sqrt{9^2 \cdot 3^2 — 9^2} = \sqrt{9^2 (3^2 — 1)} = \)
\(=\sqrt{81 (9 — 1)} = \sqrt{81 \cdot 8} = 9 \sqrt{8} = 9 \cdot 2 \sqrt{2} = 18 \sqrt{2} \) см.
Площадь основания конуса \(S_{осн}\) равна площади круга с радиусом \(r\): \( S_{осн} = \pi r^2 \).
Подставляем данное значение \(r=9\) см:
\( S_{осн} = \pi \cdot 9^2 = 81 \pi \) см\(^2\).
Дано: радиус основания конуса \(r = 9\) см, центральный угол развертки боковой поверхности \( \alpha = 120^\circ \).
Найти: высоту конуса \(H\) и площадь основания \(S_{осн}\).
Решение:
Развертка боковой поверхности конуса представляет собой круговой сектор. Площадь этого сектора равна площади боковой поверхности конуса. Площадь кругового сектора вычисляется по формуле \( S_{сектора} = \frac{\pi L^2 \alpha}{360^\circ} \), где \(L\) — радиус сектора, который является образующей конуса, и \( \alpha \) — центральный угол сектора. Площадь боковой поверхности конуса вычисляется по формуле \( S_{бок} = \pi r L \), где \(r\) — радиус основания конуса, а \(L\) — образующая конуса.
Приравниваем площади боковой поверхности: \( \frac{\pi L^2 \alpha}{360^\circ} = \pi r L \).
Подставим известные значения \(r = 9\) и \( \alpha = 120^\circ \):
\( \frac{\pi L^2 \cdot 120^\circ}{360^\circ} = \pi \cdot 9 \cdot L \).
Упростим левую часть уравнения: \( \frac{120}{360} = \frac{1}{3} \), поэтому \( \frac{\pi L^2}{3} = 9 \pi L \).
Разделим обе части уравнения на \( \pi L \) (поскольку \(L\) — образующая, она не может быть равна нулю):
\( \frac{L}{3} = 9 \).
Умножим обе части на 3, чтобы найти \(L\):
\( L = 9 \cdot 3 = 27 \) см.
Таким образом, образующая конуса равна 27 см.
Теперь найдем высоту конуса \(H\). Высота конуса, радиус основания и образующая образуют прямоугольный треугольник, где образующая является гипотенузой. По теореме Пифагора: \( H^2 + r^2 = L^2 \).
Выразим высоту \(H\): \( H = \sqrt{L^2 — r^2} \).
Подставим значения \(L = 27\) см и \(r = 9\) см:
\( H = \sqrt{27^2 — 9^2} \).
Вычислим квадраты: \( 27^2 = 729 \) и \( 9^2 = 81 \).
\( H = \sqrt{729 — 81} = \sqrt{648} \).
Разложим число 648 на множители, чтобы извлечь квадратный корень. \( 648 = 81 \cdot 8 \).
\( H = \sqrt{81 \cdot 8} = \sqrt{81} \cdot \sqrt{8} = 9 \sqrt{4 \cdot 2} = 9 \cdot 2 \sqrt{2} = 18 \sqrt{2} \) см.
Высота конуса равна \( 18 \sqrt{2} \) см.
Теперь вычислим площадь основания конуса \(S_{осн}\). Основание конуса — это круг радиусом \(r\). Площадь круга вычисляется по формуле \( S_{круга} = \pi r^2 \).
Подставим значение \(r = 9\) см:
\( S_{осн} = \pi \cdot 9^2 = \pi \cdot 81 = 81 \pi \) см\(^2\).
Площадь основания конуса равна \( 81 \pi \) см\(^2\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.