
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 359 Атанасян — Подробные Ответы
Найдите угол при вершине осевого сечения конуса, если развёрткой его боковой поверхности является сектор с дугой, равной: а) \(180^\circ\); б) \(90^\circ\); в) \(60^\circ\).
Пусть \(L\) — образующая конуса, \(r\) — радиус основания, \(H\) — высота конуса. Развертка боковой поверхности конуса представляет собой круговой сектор с радиусом \(L\) и центральным углом \( \alpha \). Длина дуги этого сектора равна длине окружности основания конуса, то есть \( \frac{\alpha}{360^\circ} \cdot 2 \pi L = 2 \pi r \). Отсюда получаем соотношение \( \frac{\alpha}{360^\circ} = \frac{r}{L} \).
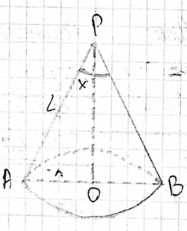
Осевое сечение конуса — равнобедренный треугольник с боковыми сторонами \(L\) и основанием \(2r\). Угол при вершине этого треугольника, который нам нужно найти, обозначим через \( \theta \). В прямоугольном треугольнике, образованном высотой конуса, радиусом основания и образующей, угол между образующей и высотой равен \( \frac{\theta}{2} \). Для этого прямоугольного треугольника справедливо соотношение \( \sin \left( \frac{\theta}{2} \right) = \frac{r}{L} \).
Приравнивая выражения для \( \frac{r}{L} \), получаем \( \sin \left( \frac{\theta}{2} \right) = \frac{\alpha}{360^\circ} \). Отсюда \( \frac{\theta}{2} = \arcsin \left( \frac{\alpha}{360^\circ} \right) \), и искомый угол при вершине осевого сечения равен \( \theta = 2 \arcsin \left( \frac{\alpha}{360^\circ} \right) \).
Теперь вычислим значение \( \theta \) для каждого случая:
а) Если \( \alpha = 180^\circ \), то \( \sin \left( \frac{\theta}{2} \right) = \frac{180^\circ}{360^\circ} = \frac{1}{2} \). Следовательно, \( \frac{\theta}{2} = 30^\circ \), и \( \theta = 2 \cdot 30^\circ = 60^\circ \).
б) Если \( \alpha = 90^\circ \), то \( \sin \left( \frac{\theta}{2} \right) = \frac{90^\circ}{360^\circ} = \frac{1}{4} \). Следовательно, \( \frac{\theta}{2} = \arcsin \left( \frac{1}{4} \right) \), и \( \theta = 2 \arcsin \left( \frac{1}{4} \right) \).
в) Если \( \alpha = 60^\circ \), то \( \sin \left( \frac{\theta}{2} \right) = \frac{60^\circ}{360^\circ} = \frac{1}{6} \). Следовательно, \( \frac{\theta}{2} = \arcsin \left( \frac{1}{6} \right) \), и \( \theta = 2 \arcsin \left( \frac{1}{6} \right) \).
Пусть \(L\) обозначает образующую конуса, а \(r\) — радиус его основания. Развертка боковой поверхности конуса представляет собой круговой сектор с радиусом, равным образующей конуса \(L\), и центральным углом \( \alpha \). Длина дуги этого сектора равна длине окружности основания конуса. Длина окружности основания конуса вычисляется по формуле \(C = 2 \pi r\). Длина дуги кругового сектора с радиусом \(L\) и центральным углом \( \alpha \) (в градусах) равна \( \frac{\alpha}{360^\circ} \cdot 2 \pi L \). Приравнивая эти длины, получаем уравнение \( \frac{\alpha}{360^\circ} \cdot 2 \pi L = 2 \pi r \). Сокращая \(2 \pi\) с обеих сторон и деля на \(L\), получаем соотношение \( \frac{\alpha}{360^\circ} = \frac{r}{L} \).
Осевое сечение конуса представляет собой равнобедренный треугольник, у которого боковые стороны равны образующей конуса \(L\), а основание равно диаметру основания конуса \(2r\). Угол при вершине этого равнобедренного треугольника является искомым углом осевого сечения. Обозначим половину этого угла через \(x\). Рассмотрим прямоугольный треугольник, образованный высотой конуса, радиусом основания \(r\) и образующей \(L\). В этом треугольнике угол между образующей и высотой равен \(x\). По определению синуса в прямоугольном треугольнике, \( \sin x = \frac{\text{противолежащий катет}}{\text{гипотенуза}} = \frac{r}{L} \).
Таким образом, мы получили два выражения для отношения \( \frac{r}{L} \): \( \frac{r}{L} = \frac{\alpha}{360^\circ} \) и \( \frac{r}{L} = \sin x \). Приравнивая их, находим связь между углом развертки \( \alpha \) и половиной угла осевого сечения \(x\): \( \sin x = \frac{\alpha}{360^\circ} \). Искомый угол при вершине осевого сечения равен \(2x\).
Рассмотрим три случая, заданные в условии:
а) Угол развертки боковой поверхности \( \alpha = 180^\circ \). Подставляем это значение в соотношение для \( \sin x \): \( \sin x = \frac{180^\circ}{360^\circ} = \frac{1}{2} \). Известно, что \( \sin 30^\circ = \frac{1}{2} \), поэтому \( x = 30^\circ \). Угол при вершине осевого сечения равен \( 2x = 2 \cdot 30^\circ = 60^\circ \).
б) Угол развертки боковой поверхности \( \alpha = 90^\circ \). Подставляем это значение в соотношение для \( \sin x \): \( \sin x = \frac{90^\circ}{360^\circ} = \frac{1}{4} \). Для нахождения \(x\) используем обратную тригонометрическую функцию арксинус: \( x = \arcsin \left( \frac{1}{4} \right) \). Угол при вершине осевого сечения равен \( 2x = 2 \arcsin \left( \frac{1}{4} \right) \).
в) Угол развертки боковой поверхности \( \alpha = 60^\circ \). Подставляем это значение в соотношение для \( \sin x \): \( \sin x = \frac{60^\circ}{360^\circ} = \frac{1}{6} \). Для нахождения \(x\) используем обратную тригонометрическую функцию арксинус: \( x = \arcsin \left( \frac{1}{6} \right) \). Угол при вершине осевого сечения равен \( 2x = 2 \arcsin \left( \frac{1}{6} \right) \).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!