Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 358 Атанасян — Подробные Ответы
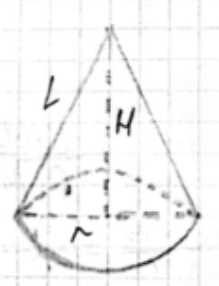
Найдите дугу сектора, представляющего собой развёртку боковой поверхности конуса, если образующая конуса составляет с плоскостью основания угол в \(60^\circ\).
Радиус основания конуса равен \(r = L \cos 60^\circ = L \cdot \frac{1}{2} = \frac{L}{2}\). Площадь боковой поверхности конуса равна \(S_{бок} = \pi r L\). Развертка боковой поверхности представляет собой круговой сектор с радиусом \(L\) и углом \( \alpha \).
Площадь этого сектора равна \(S_{сектор} = \frac{\pi L^2 \alpha}{360^\circ}\). Приравнивая площади, получаем \( \frac{\pi L^2 \alpha}{360^\circ} = \pi r L \). Отсюда выражаем \( \alpha \): \( \alpha = \frac{360^\circ \pi r L}{\pi L^2} = \frac{360^\circ r}{L} \). Подставляя \( r = \frac{L}{2} \), находим \( \alpha = \frac{360^\circ (L/2)}{L} = \frac{360^\circ}{2} = 180^\circ \).
Дано: конус, образующая \(L\), угол между образующей и плоскостью основания составляет \(60^\circ\). Требуется найти градусную меру угла \( \alpha \) развертки боковой поверхности конуса.
Решение:
Рассмотрим прямоугольный треугольник, образованный образующей конуса \(L\), радиусом основания \(r\) и высотой конуса \(H\). Угол между образующей и плоскостью основания равен \(60^\circ\). В этом прямоугольном треугольнике радиус основания \(r\) является прилежащим катетом к углу \(60^\circ\), а образующая \(L\) является гипотенузой. Используя определение косинуса в прямоугольном треугольнике, получаем соотношение \( \cos 60^\circ = \frac{r}{L} \).
Из этого соотношения выразим радиус основания \(r\): \( r = L \cos 60^\circ \). Поскольку \( \cos 60^\circ = \frac{1}{2} \), получаем \( r = L \cdot \frac{1}{2} = \frac{L}{2} \).
Боковая поверхность конуса при развертке на плоскость представляет собой круговой сектор. Радиус этого сектора равен образующей конуса \(L\). Длина дуги этого сектора равна длине окружности основания конуса. Длина окружности основания конуса вычисляется по формуле \( C = 2 \pi r \). Подставляя найденное значение \( r = \frac{L}{2} \), получаем \( C = 2 \pi \left( \frac{L}{2} \right) = \pi L \).
Длина дуги кругового сектора с радиусом \(L\) и центральным углом \( \alpha \) (измеренным в градусах) вычисляется по формуле \( \text{Длина дуги} = \frac{\alpha}{360^\circ} \cdot 2 \pi L \).
Приравнивая длину дуги сектора к длине окружности основания конуса, получаем уравнение: \( \frac{\alpha}{360^\circ} \cdot 2 \pi L = \pi L \).
Теперь решим это уравнение относительно \( \alpha \). Для этого разделим обе части уравнения на \( \pi L \) (при условии, что \( L \neq 0 \), что верно для конуса): \( \frac{\alpha}{360^\circ} \cdot 2 = 1 \).
Далее, умножим обе части на \( 360^\circ \): \( \alpha \cdot 2 = 360^\circ \).
Наконец, разделим обе части на 2, чтобы найти \( \alpha \): \( \alpha = \frac{360^\circ}{2} = 180^\circ \).
Таким образом, градусная мера угла развертки боковой поверхности конуса составляет \(180^\circ\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.