Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 357 Атанасян — Подробные Ответы
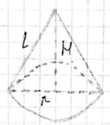
Развёрткой боковой поверхности конуса является сектор с дугой \(\alpha\). Найдите \(\alpha\), если высота конуса равна 4 см, а радиус основания равен 3 см.
Дано: радиус основания конуса \(r = 3\) см, высота конуса \(h = 4\) см. Найдем образующую конуса \(L\) по теореме Пифагора: \(L = \sqrt{r^2 + h^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\) см.
Развертка боковой поверхности конуса представляет собой круговой сектор с радиусом, равным образующей конуса \(L\), и длиной дуги, равной длине окружности основания конуса \(2\pi r\). Длина дуги сектора также выражается формулой \(\frac{\alpha}{360^\circ} \cdot 2\pi L\), где \(\alpha\) — искомый угол сектора. Приравниваем длины дуг: \(2\pi r = \frac{\alpha}{360^\circ} \cdot 2\pi L\). Сокращаем \(2\pi\) с обеих сторон: \(r = \frac{\alpha}{360^\circ} \cdot L\). Выражаем \(\alpha\): \(\alpha = \frac{r \cdot 360^\circ}{L}\). Подставляем значения \(r=3\) и \(L=5\): \(\alpha = \frac{3 \cdot 360^\circ}{5} = \frac{1080^\circ}{5} = 216^\circ\). Ответ: \(\alpha = 216^\circ\).
Дано: радиус основания конуса \(r = 3\) см, высота конуса \(h = 4\) см. Требуется найти угол \(\alpha\) развертки боковой поверхности конуса.
Первым шагом найдем образующую \(L\) конуса. Образующая, радиус основания и высота конуса образуют прямоугольный треугольник, где образующая является гипотенузой. По теореме Пифагора квадрат образующей равен сумме квадратов радиуса и высоты: \(L^2 = r^2 + h^2\). Подставляем данные значения: \(L^2 = 3^2 + 4^2\). Вычисляем квадраты: \(3^2 = 9\) и \(4^2 = 16\). Складываем их: \(L^2 = 9 + 16 = 25\). Извлекаем квадратный корень, чтобы найти \(L\): \(L = \sqrt{25} = 5\). Таким образом, образующая конуса равна \(5\) см.
Вторым шагом рассмотрим развертку боковой поверхности конуса. Разверткой является круговой сектор. Радиус этого сектора равен образующей конуса \(L\). Длина дуги этого сектора равна длине окружности основания конуса.
Третьим шагом вычислим длину окружности основания конуса. Длина окружности с радиусом \(r\) вычисляется по формуле \(C = 2\pi r\). Подставляем значение радиуса \(r = 3\) см: \(C = 2\pi \cdot 3 = 6\pi\) см.
Четвертым шагом выразим длину дуги кругового сектора с радиусом \(L\) и центральным углом \(\alpha\) (в градусах). Формула для длины дуги сектора: \(Arc Length = \frac{\alpha}{360^\circ} \cdot 2\pi L\). Подставляем радиус сектора, равный образующей конуса \(L = 5\) см: \(Arc Length = \frac{\alpha}{360^\circ} \cdot 2\pi \cdot 5 = \frac{10\pi \alpha}{360^\circ}\).
Пятым шагом приравняем длину дуги развертки к длине окружности основания конуса, так как это одна и та же величина: \(6\pi = \frac{10\pi \alpha}{360^\circ}\).
Шестым шагом решим полученное уравнение относительно \(\alpha\). Уравнение: \(6\pi = \frac{10\pi \alpha}{360^\circ}\). Разделим обе части уравнения на \(\pi\) (поскольку \(\pi \neq 0\)): \(6 = \frac{10 \alpha}{360^\circ}\). Упростим дробь в правой части, разделив числитель и знаменатель на \(10\): \(6 = \frac{\alpha}{36^\circ}\). Чтобы найти \(\alpha\), умножим обе части уравнения на \(36^\circ\): \(\alpha = 6 \cdot 36^\circ\). Выполняем умножение: \(6 \cdot 36 = 216\). Таким образом, \(\alpha = 216^\circ\).
Угол развертки боковой поверхности конуса равен \(216^\circ\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.