
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 356 Атанасян — Подробные Ответы
Две секущие плоскости перпендикулярны к оси конуса. Докажите, что площади сечений конуса этими плоскостями относятся как квадраты расстояний от вершины конуса до этих плоскостей.
Решение: Возьмем рисунок из задачи №56. Из подобия треугольников следует, что \(\frac{O_1M_1}{O_2M_2} = \frac{PO_1}{PO_2}\), или \(\frac{r_1}{r_2} = \frac{PO_1}{PO_2}\), где \(r_1\) и \(r_2\) — радиусы сечений, а \(PO_1\) и \(PO_2\) — расстояния от вершины конуса до плоскостей сечений.
Площади сечений равны \(S_1 = \pi r_1^2\) и \(S_2 = \pi r_2^2\). Возводя в квадрат отношение радиусов, получаем \(\frac{r_1^2}{r_2^2} = \frac{PO_1^2}{PO_2^2}\). Умножая обе части на \(\pi\), имеем \(\frac{\pi r_1^2}{\pi r_2^2} = \frac{PO_1^2}{PO_2^2}\). Таким образом, \(\frac{S_1}{S_2} = \frac{PO_1^2}{PO_2^2}\), что и требовалось доказать.
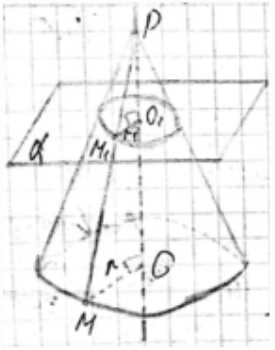
Пусть дан конус с вершиной P, основанием которого является круг с центром O и радиусом r. Ось конуса — отрезок PO. Секущая плоскость \(\alpha\) перпендикулярна к оси конуса и пересекает ее в точке O\(_1\). Требуется доказать, что сечение конуса плоскостью \(\alpha\) представляет собой круг с центром O\(_1\) и радиусом \(r_1\), где \(r_1 = \frac{PO_1}{PO}r\).
Для доказательства рассмотрим две части.
Первая часть: Докажем, что любая точка M\(_1\), лежащая в плоскости \(\alpha\) и на окружности радиуса \(r_1\) с центром O\(_1\), принадлежит сечению конуса, то есть лежит на некоторой образующей конуса.
Рассмотрим произвольную точку M\(_1\) в плоскости \(\alpha\) такую, что расстояние от O\(_1\) до M\(_1\) равно \(r_1\), то есть \(O_1M_1 = r_1\). Проведем луч PM\(_1\) из вершины конуса P через точку M\(_1\). Этот луч пересечет плоскость основания конуса в некоторой точке M. Рассмотрим треугольники PO\(_1\)M\(_1\) и POM. Поскольку плоскость \(\alpha\) перпендикулярна оси PO, треугольник PO\(_1\)M\(_1\) является прямоугольным с прямым углом при вершине O\(_1\). Плоскость основания перпендикулярна оси PO, поэтому треугольник POM является прямоугольным с прямым углом при вершине O. Угол при вершине P является общим для обоих треугольников. Следовательно, прямоугольные треугольники PO\(_1\)M\(_1\) и POM подобны по двум углам (общему острому углу P и прямым углам при O\(_1\) и O).
Из подобия этих треугольников следует пропорциональность соответствующих сторон: \(\frac{O_1M_1}{OM} = \frac{PO_1}{PO}\).
Подставим в это соотношение \(O_1M_1 = r_1\): \(\frac{r_1}{OM} = \frac{PO_1}{PO}\).
Выразим OM: \(OM = \frac{PO}{PO_1} \cdot r_1\).
По условию радиус сечения \(r_1\) связан с радиусом основания r соотношением \(r_1 = \frac{PO_1}{PO}r\). Подставим это выражение для \(r_1\) в формулу для OM: \(OM = \frac{PO}{PO_1} \cdot \left(\frac{PO_1}{PO}r\right)\).
Сокращая \(\frac{PO}{PO_1}\) и \(\frac{PO_1}{PO}\), получаем \(OM = r\).
Это означает, что точка M лежит на окружности основания конуса. Поскольку точка M лежит на окружности основания, отрезок PM является образующей конуса. Точка M\(_1\) лежит на отрезке PM (так как M\(_1\) лежит на луче PM\(_1\)), а значит, точка M\(_1\) лежит на образующей конуса. Поскольку M\(_1\) также лежит в плоскости \(\alpha\), она является точкой сечения конуса плоскостью \(\alpha\).
Вторая часть: Докажем, что любая точка M\(_1\), принадлежащая сечению конуса (то есть лежащая как в плоскости \(\alpha\), так и на боковой поверхности конуса), лежит на окружности радиуса \(r_1\) с центром O\(_1\).
Рассмотрим произвольную точку M\(_1\), которая лежит в плоскости \(\alpha\) и на боковой поверхности конуса. Поскольку M\(_1\) лежит на боковой поверхности конуса, она лежит на некоторой образующей PM, где M — точка на окружности основания конуса. Следовательно, расстояние от O до M равно радиусу основания r, то есть \(OM = r\).
Рассмотрим снова треугольники PO\(_1\)M\(_1\) и POM. Как было показано ранее, эти треугольники подобны, так как они прямоугольные (при O\(_1\) и O) и имеют общий угол P.
Из подобия этих треугольников следует пропорциональность соответствующих сторон: \(\frac{O_1M_1}{OM} = \frac{PO_1}{PO}\).
Выразим \(O_1M_1\): \(O_1M_1 = \frac{PO_1}{PO} \cdot OM\).
Подставим в это соотношение \(OM = r\): \(O_1M_1 = \frac{PO_1}{PO} \cdot r\).
По определению радиуса сечения \(r_1 = \frac{PO_1}{PO}r\). Таким образом, мы получили, что \(O_1M_1 = r_1\).
Это означает, что расстояние от точки M\(_1\) до точки O\(_1\) равно \(r_1\). Поскольку точка M\(_1\) лежит в плоскости \(\alpha\), она лежит на окружности радиуса \(r_1\) с центром O\(_1\) в этой плоскости.
Из обеих частей доказательства следует, что множество точек сечения конуса плоскостью \(\alpha\) совпадает с окружностью радиуса \(r_1\) с центром O\(_1\) в плоскости \(\alpha\). Следовательно, сечение конуса плоскостью \(\alpha\) представляет собой круг, границей которого является эта окружность.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!