ГДЗ по Геометрии 10 класс Номер 354 Атанасян — Подробные Ответы

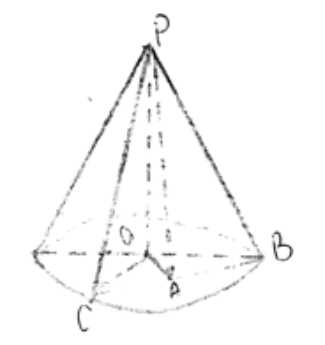
Высота конуса равна 10 см. Найдите площадь сечения, проходящего через вершину конуса и хорду основания, стягивающую дугу в \(60^\circ\), если плоскость сечения образует с плоскостью основания конуса угол: а) \(30^\circ\); б) \(45^\circ\); в) \(60^\circ\).

Решение:
Высота конуса \(PO = h = 10\) см. Хорда \(BC\) стягивает дугу \(60^\circ\), значит центральный угол \(\angle COB = 60^\circ\). Поскольку \(OC = OB = r\), треугольник \(COB\) равнобедренный. Так как \(\angle COB = 60^\circ\), треугольник \(COB\) равносторонний, и \(BC = OC = OB = r\). Проведем \(OA \perp BC\), где \(A\) — середина \(BC\). По теореме о трех перпендикулярах, \(PA \perp BC\). Угол между плоскостью сечения \(PBC\) и плоскостью основания равен \(\angle PAO\). Площадь сечения \(S_{PBC} = \frac{1}{2} \cdot BC \cdot PA\).

а) Если \(\angle PAO = 30^\circ\). В прямоугольном треугольнике \(POA\), \(PA = \frac{PO}{\sin 30^\circ} = \frac{h}{1/2} = 2h\). В равностороннем треугольнике \(COB\), \(OA\) — высота, \(OA = OC \cos 30^\circ = r \frac{\sqrt{3}}{2}\). В прямоугольном треугольнике \(POA\), \(\tan 30^\circ = \frac{PO}{OA}\), \(OA = \frac{h}{\tan 30^\circ} = \frac{h}{1/\sqrt{3}} = h\sqrt{3}\). Приравнивая выражения для \(OA\), \(r \frac{\sqrt{3}}{2} = h\sqrt{3}\), откуда \(r = 2h\). \(BC = r = 2h\). Площадь сечения \(S_{PBC} = \frac{1}{2} \cdot (2h) \cdot (2h) = 2h^2\). При \(h = 10\) см, \(S_{PBC} = 2 \cdot 10^2 = 200\) см\(^2\).

б) Если \(\angle PAO = 45^\circ\). В прямоугольном треугольнике \(POA\), \(PA = \frac{PO}{\sin 45^\circ} = \frac{h}{1/\sqrt{2}} = h\sqrt{2}\). \(\triangle POA\) равнобедренный, \(OA = PO = h\). Из \(OA = r \frac{\sqrt{3}}{2}\) следует \(h = r \frac{\sqrt{3}}{2}\), откуда \(r = \frac{2h}{\sqrt{3}}\). \(BC = r = \frac{2h}{\sqrt{3}}\). Площадь сечения \(S_{PBC} = \frac{1}{2} \cdot \left(\frac{2h}{\sqrt{3}}\right) \cdot (h\sqrt{2}) = \frac{h^2\sqrt{2}}{\sqrt{3}} = \frac{h^2\sqrt{6}}{3}\). При \(h = 10\) см, \(S_{PBC} = \frac{100\sqrt{6}}{3}\) см\(^2\).

в) Если \(\angle PAO = 60^\circ\). В прямоугольном треугольнике \(POA\), \(PA = \frac{PO}{\sin 60^\circ} = \frac{h}{\sqrt{3}/2} = \frac{2h}{\sqrt{3}}\). \(OA = \frac{PO}{\tan 60^\circ} = \frac{h}{\sqrt{3}}\). Из \(OA = r \frac{\sqrt{3}}{2}\) следует \(\frac{h}{\sqrt{3}} = r \frac{\sqrt{3}}{2}\), откуда \(r = \frac{2h}{3}\). \(BC = r = \frac{2h}{3}\). Площадь сечения \(S_{PBC} = \frac{1}{2} \cdot \left(\frac{2h}{3}\right) \cdot \left(\frac{2h}{\sqrt{3}}\right) = \frac{2h^2}{3\sqrt{3}} = \frac{2h^2\sqrt{3}}{9}\). При \(h = 10\) см, \(S_{PBC} = \frac{2 \cdot 10^2\sqrt{3}}{9} = \frac{200\sqrt{3}}{9}\) см\(^2\).

Дано: высота конуса \(h = PO = 10\) см. \(BC\) — хорда основания. Угол \(\angle COB = 60^\circ\). Найти площадь сечения \(S_{PBC}\).

Решение:
Основание конуса представляет собой окружность с центром в точке \(O\). Хорда \(BC\) стягивает дугу в \(60^\circ\), следовательно, центральный угол, опирающийся на эту дугу, \(\angle COB = 60^\circ\). Поскольку \(OC\) и \(OB\) являются радиусами основания, \(OC = OB = r\). Треугольник \(COB\) является равнобедренным с углом при вершине \(60^\circ\), поэтому он является равносторонним. Таким образом, длина хорды \(BC\) равна радиусу основания, \(BC = r\).

Проведем отрезок \(OA\) перпендикулярно хорде \(BC\), где точка \(A\) лежит на хорде \(BC\). В равностороннем треугольнике \(COB\), \(OA\) является высотой, медианой и биссектрисой угла \(\angle COB\). Следовательно, \(A\) является серединой \(BC\), и \(\angle COA = \frac{1}{2} \angle COB = \frac{1}{2} \cdot 60^\circ = 30^\circ\). В прямоугольном треугольнике \(COA\) с прямым углом при вершине \(A\), длина отрезка \(OA\) может быть найдена как \(OA = OC \cos(\angle COA) = r \cos 30^\circ = r \frac{\sqrt{3}}{2}\).

Сечение, проходящее через вершину конуса \(P\) и хорду \(BC\), представляет собой треугольник \(PBC\). Высота конуса \(PO\) перпендикулярна плоскости основания. Поскольку \(OA \perp BC\) в плоскости основания, по теореме о трех перпендикулярах, наклонная \(PA\) также перпендикулярна \(BC\). Таким образом, \(PA\) является высотой треугольника сечения \(PBC\), опущенной на основание \(BC\). Площадь сечения \(S_{PBC}\) вычисляется по формуле площади треугольника: \(S_{PBC} = \frac{1}{2} \cdot BC \cdot PA\).

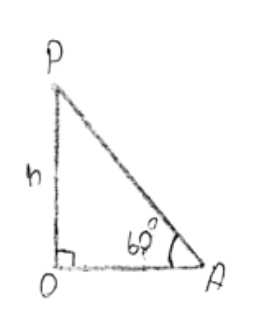
Угол между плоскостью сечения \(PBC\) и плоскостью основания конуса — это линейный угол двугранного угла, образованного этими плоскостями. Поскольку \(OA \perp BC\) и \(PA \perp BC\), линейным углом является угол \(\angle PAO\). Треугольник \(POA\) является прямоугольным с прямым углом при вершине \(O\), так как \(PO\) — высота конуса. В этом прямоугольном треугольнике мы можем использовать тригонометрические соотношения.

а) Если угол между плоскостью сечения и плоскостью основания равен \(30^\circ\), то \(\angle PAO = 30^\circ\).
В прямоугольном треугольнике \(POA\):
Длина отрезка \(PA\) находится из соотношения \(\sin(\angle PAO) = \frac{PO}{PA}\), откуда \(PA = \frac{PO}{\sin(\angle PAO)} = \frac{h}{\sin 30^\circ} = \frac{h}{1/2} = 2h\).
Длина отрезка \(OA\) находится из соотношения \(\tan(\angle PAO) = \frac{PO}{OA}\), откуда \(OA = \frac{PO}{\tan(\angle PAO)} = \frac{h}{\tan 30^\circ} = \frac{h}{1/\sqrt{3}} = h\sqrt{3}\).
Мы также знаем, что \(OA = r \frac{\sqrt{3}}{2}\). Приравнивая два выражения для \(OA\), получаем \(h\sqrt{3} = r \frac{\sqrt{3}}{2}\), откуда \(r = 2h\).
Длина хорды \(BC = r = 2h\).
Теперь вычислим площадь сечения \(S_{PBC} = \frac{1}{2} \cdot BC \cdot PA = \frac{1}{2} \cdot (2h) \cdot (2h) = 2h^2\).
Подставляя значение \(h = 10\) см, получаем \(S_{PBC} = 2 \cdot (10)^2 = 2 \cdot 100 = 200\) см\(^2\).

б) Если угол между плоскостью сечения и плоскостью основания равен \(45^\circ\), то \(\angle PAO = 45^\circ\).
В прямоугольном треугольнике \(POA\):
Длина отрезка \(PA = \frac{PO}{\sin 45^\circ} = \frac{h}{1/\sqrt{2}} = h\sqrt{2}\).
Длина отрезка \(OA = \frac{PO}{\tan 45^\circ} = \frac{h}{1} = h\).
Приравнивая \(OA = h\) и \(OA = r \frac{\sqrt{3}}{2}\), получаем \(h = r \frac{\sqrt{3}}{2}\), откуда \(r = \frac{2h}{\sqrt{3}}\).
Длина хорды \(BC = r = \frac{2h}{\sqrt{3}}\).
Площадь сечения \(S_{PBC} = \frac{1}{2} \cdot BC \cdot PA = \frac{1}{2} \cdot \left(\frac{2h}{\sqrt{3}}\right) \cdot (h\sqrt{2}) = \frac{h^2\sqrt{2}}{\sqrt{3}} = \frac{h^2\sqrt{6}}{3}\).
Подставляя значение \(h = 10\) см, получаем \(S_{PBC} = \frac{(10)^2\sqrt{6}}{3} = \frac{100\sqrt{6}}{3}\) см\(^2\).

в) Если угол между плоскостью сечения и плоскостью основания равен \(60^\circ\), то \(\angle PAO = 60^\circ\).
В прямоугольном треугольнике \(POA\):
Длина отрезка \(PA = \frac{PO}{\sin 60^\circ} = \frac{h}{\sqrt{3}/2} = \frac{2h}{\sqrt{3}}\).
Длина отрезка \(OA = \frac{PO}{\tan 60^\circ} = \frac{h}{\sqrt{3}}\).
Приравнивая \(OA = \frac{h}{\sqrt{3}}\) и \(OA = r \frac{\sqrt{3}}{2}\), получаем \(\frac{h}{\sqrt{3}} = r \frac{\sqrt{3}}{2}\), откуда \(r = \frac{2h}{3}\).
Длина хорды \(BC = r = \frac{2h}{3}\).
Площадь сечения \(S_{PBC} = \frac{1}{2} \cdot BC \cdot PA = \frac{1}{2} \cdot \left(\frac{2h}{3}\right) \cdot \left(\frac{2h}{\sqrt{3}}\right) = \frac{2h^2}{3\sqrt{3}} = \frac{2h^2\sqrt{3}}{9}\).
Подставляя значение \(h = 10\) см, получаем \(S_{PBC} = \frac{2 \cdot (10)^2\sqrt{3}}{9} = \frac{2 \cdot 100\sqrt{3}}{9} = \frac{200\sqrt{3}}{9}\) см\(^2\).