
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 353 Атанасян — Подробные Ответы
Образующая конуса равна l, а радиус основания равен r. Найдите площадь сечения, проходящего через вершину конуса и хорду основания, стягивающую дугу: а) в \(60^\circ\); б) в \(90^\circ\).
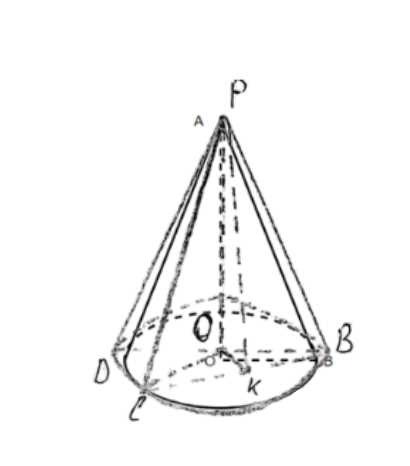
Дано: конус с образующей \(l\) и радиусом основания \(r\). BC — хорда основания. Найти площадь сечения (треугольника PBC), проходящего через вершину P и хорду BC. Площадь сечения находится по формуле \(S_{PBC} = \frac{1}{2} \cdot BC \cdot PK\), где PK — высота треугольника PBC, проведенная из вершины P к основанию BC. PK перпендикулярна BC по теореме о трех перпендикулярах, так как OK перпендикулярна BC (OK — радиус, перпендикулярный хорде) и PO перпендикулярна плоскости основания.
а) Хорда BC стягивает дугу в \(60^\circ\). Центральный угол, соответствующий этой дуге, равен \(60^\circ\). Треугольник BOC равнобедренный с OB = OC = r. Так как угол BOC = \(60^\circ\), треугольник BOC равносторонний, следовательно, \(BC = r\). В прямоугольном треугольнике CPK (где K — середина BC), \(CK = \frac{BC}{2} = \frac{r}{2}\). По теореме Пифагора в треугольнике CPK: \(PK^2 = PC^2 — CK^2 = l^2 — (\frac{r}{2})^2 = l^2 — \frac{r^2}{4} = \frac{4l^2 — r^2}{4}\). Отсюда \(PK = \sqrt{\frac{4l^2 — r^2}{4}} = \frac{\sqrt{4l^2 — r^2}}{2}\). Площадь сечения: \(S_{PBC} = \frac{1}{2} \cdot BC \cdot PK = \frac{1}{2} \cdot r \cdot \frac{\sqrt{4l^2 — r^2}}{2} = \frac{r\sqrt{4l^2 — r^2}}{4}\).
б) Хорда BC стягивает дугу в \(90^\circ\). Центральный угол, соответствующий этой дуге, равен \(90^\circ\). Треугольник BOC равнобедренный с OB = OC = r и углом BOC = \(90^\circ\). По теореме Пифагора в треугольнике BOC: \(BC^2 = OB^2 + OC^2 = r^2 + r^2 = 2r^2\). Следовательно, \(BC = \sqrt{2}r\). В прямоугольном треугольнике CPK, \(CK = \frac{BC}{2} = \frac{\sqrt{2}r}{2} = \frac{r}{\sqrt{2}}\). По теореме Пифагора в треугольнике CPK: \(PK^2 = PC^2 — CK^2 = l^2 — (\frac{r}{\sqrt{2}})^2 = l^2 — \frac{r^2}{2} = \frac{2l^2 — r^2}{2}\). Отсюда \(PK = \sqrt{\frac{2l^2 — r^2}{2}} = \frac{\sqrt{2l^2 — r^2}}{\sqrt{2}}\). Площадь сечения: \(S_{PBC} = \frac{1}{2} \cdot BC \cdot PK = \frac{1}{2} \cdot \sqrt{2}r \cdot \frac{\sqrt{2l^2 — r^2}}{\sqrt{2}} = \frac{1}{2} r \sqrt{2l^2 — r^2}\).
Рассмотрим конус с вершиной P, основанием с центром O и радиусом r. Образующая конуса равна l. Сечение, проходящее через вершину P и хорду BC основания, представляет собой треугольник PBC. Площадь этого треугольника можно найти по формуле \(S_{PBC} = \frac{1}{2} \cdot BC \cdot PK\), где BC — длина хорды, а PK — высота треугольника PBC, опущенная из вершины P на хорду BC.
Проведем радиус OK перпендикулярно хорде BC. K является серединой хорды BC. Так как PO — высота конуса (перпендикулярна плоскости основания) и OK перпендикулярна BC в плоскости основания, то по теореме о трех перпендикулярах, PK перпендикулярна BC. Следовательно, PK является высотой треугольника PBC.
а) Хорда BC стягивает дугу в \(60^\circ\).
Центральный угол \( \angle BOC \) равен угловой мере дуги, которую стягивает хорда, то есть \( \angle BOC = 60^\circ \). Треугольник BOC является равнобедренным, так как OB = OC = r (радиусы основания). Поскольку угол при вершине O равен \(60^\circ\), а углы при основании равнобедренного треугольника равны, то \( \angle OBC = \angle OCB = \frac{180^\circ — 60^\circ}{2} = 60^\circ \). Таким образом, треугольник BOC является равносторонним, и длина хорды BC равна радиусу основания: \( BC = r \).
K — середина BC, поэтому \( CK = \frac{BC}{2} = \frac{r}{2} \).
В прямоугольном треугольнике CPK (где PC — образующая конуса, PC = l), по теореме Пифагора найдем высоту PK:
\( PK^2 = PC^2 — CK^2 \)
\( PK^2 = l^2 — (\frac{r}{2})^2 \)
\( PK^2 = l^2 — \frac{r^2}{4} \)
\( PK^2 = \frac{4l^2 — r^2}{4} \)
\( PK = \sqrt{\frac{4l^2 — r^2}{4}} = \frac{\sqrt{4l^2 — r^2}}{2} \)
Теперь найдем площадь сечения PBC:
\( S_{PBC} = \frac{1}{2} \cdot BC \cdot PK \)
\( S_{PBC} = \frac{1}{2} \cdot r \cdot \frac{\sqrt{4l^2 — r^2}}{2} \)
\( S_{PBC} = \frac{r\sqrt{4l^2 — r^2}}{4} \)
б) Хорда BC стягивает дугу в \(90^\circ\).
Центральный угол \( \angle BOC \) равен \(90^\circ\). Треугольник BOC является равнобедренным прямоугольным треугольником с катетами OB = OC = r. По теореме Пифагора найдем длину хорды BC:
\( BC^2 = OB^2 + OC^2 \)
\( BC^2 = r^2 + r^2 \)
\( BC^2 = 2r^2 \)
\( BC = \sqrt{2r^2} = r\sqrt{2} \)
K — середина BC, поэтому \( CK = \frac{BC}{2} = \frac{r\sqrt{2}}{2} = \frac{r}{\sqrt{2}} \).
В прямоугольном треугольнике CPK (где PC = l), по теореме Пифагора найдем высоту PK:
\( PK^2 = PC^2 — CK^2 \)
\( PK^2 = l^2 — (\frac{r}{\sqrt{2}})^2 \)
\( PK^2 = l^2 — \frac{r^2}{2} \)
\( PK^2 = \frac{2l^2 — r^2}{2} \)
\( PK = \sqrt{\frac{2l^2 — r^2}{2}} = \frac{\sqrt{2l^2 — r^2}}{\sqrt{2}} \)
Теперь найдем площадь сечения PBC:
\( S_{PBC} = \frac{1}{2} \cdot BC \cdot PK \)
\( S_{PBC} = \frac{1}{2} \cdot r\sqrt{2} \cdot \frac{\sqrt{2l^2 — r^2}}{\sqrt{2}} \)
\( S_{PBC} = \frac{1}{2} r \sqrt{2l^2 — r^2} \)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!