
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 35 Атанасян — Подробные Ответы
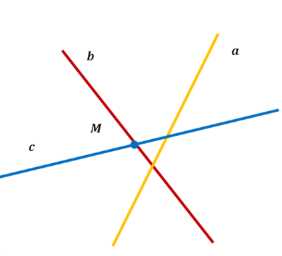
Через точку \(M\), не лежащую на прямой \(a\), проведены две прямые, не имеющие общих точек с прямой \(a\). Докажите, что по крайней мере одна из этих прямых и прямая \(a\) являются скрещивающимися прямыми.
Пусть \(a\) и \(b\) не скрещивающиеся, а также \(a\) и \(c\) не скрещивающиеся. Это означает, что \(a \parallel b\) и \(a \parallel c\) (так как прямые \(a\), \(b\), \(c\) не пересекаются). Тогда из свойства параллельных прямых следует, что \(b \parallel c\).
Однако \(b\) и \(c\) пересекаются в точке \(M\), то есть \(b \cap c = M\). Это противоречие. Следовательно, наше предположение неверно, и по крайней мере одна из пар прямых \((a, b)\) или \((a, c)\) является парой скрещивающихся прямых.
Что и требовалось доказать.
Рассмотрим точку \(M\), которая не лежит на прямой \(a\). Через \(M\) проведены две прямые \(b\) и \(c\), которые также не пересекают прямую \(a\). Требуется доказать, что либо \(a\) и \(b\), либо \(a\) и \(c\) являются скрещивающимися прямыми.
Предположим противное: ни \(a\) и \(b\), ни \(a\) и \(c\) не являются скрещивающимися. Это означает, что \(a\) и \(b\), а также \(a\) и \(c\) либо пересекаются, либо параллельны.
1. Если \(a \parallel b\) и \(a \parallel c\), то, по свойству параллельных прямых, \(b \parallel c\) (две прямые, параллельные одной и той же прямой, параллельны друг другу). Однако это противоречит условию, что прямые \(b\) и \(c\) пересекаются в точке \(M\), так как \(b \cap c = M\).
2. Если \(a\) пересекает \(b\) в некоторой точке \(P\), то \(P \in a \cap b\). Но прямая \(b\) проходит через точку \(M\), которая, по условию, не лежит на \(a\). Это противоречие, так как \(b\) не может одновременно пересекать \(a\) и проходить через \(M\), не лежащую на \(a\).
3. Аналогично, если \(a\) пересекает \(c\) в точке \(Q\), то \(Q \in a \cap c\). Но \(c\) также проходит через точку \(M\), которая не лежит на \(a\). Это снова противоречие.
Таким образом, наше предположение о том, что ни \(a\) и \(b\), ни \(a\) и \(c\) не являются скрещивающимися, неверно. Следовательно, по крайней мере одна из пар прямых \((a, b)\) или \((a, c)\) является парой скрещивающихся прямых.
Что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!