Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 349 Атанасян — Подробные Ответы
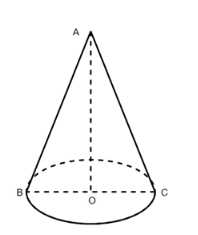
Осевое сечение конуса — прямоугольный треугольник. Найдите площадь этого сечения, если радиус основания конуса равен 5 см.
Дано \(\angle BAC = 90^\circ\), \(BC = 2R = 10\) см, \(AB = AC\).
Из \(\sqrt{AB^2 + AC^2} = BC\) следует \(\sqrt{AB^2 + AB^2} = 10\), что дает \(\sqrt{2AB^2} = 10\) или \(AB\sqrt{2} = 10\). Отсюда \(AB = \frac{10}{\sqrt{2}} = 5\sqrt{2}\) см. Так как O центр основания, \(OB = \frac{BC}{2} = \frac{10}{2} = 5\) см. В прямоугольном треугольнике AOB по теореме Пифагора \(AO^2 + OB^2 = AB^2\), то есть \(AO^2 + 5^2 = (5\sqrt{2})^2\). Получаем \(AO^2 + 25 = 50\), откуда \(AO^2 = 25\) и \(AO = 5\) см. Следовательно, \(AO \cdot OB = 5 \cdot 5 = 25\) см².
Дано, что в конусе угол при вершине \(A\) в осевом сечении \(\angle BAC = 90^\circ\), а хорда \(BC\) равна диаметру основания \(2R\) и составляет 10 см. Также известно, что образующие \(AB\) и \(AC\) равны (\(AB = AC\)). Поскольку осевое сечение является равнобедренным треугольником \(ABC\) с углом при вершине \(90^\circ\), он является прямоугольным и равнобедренным.
Первый шаг — найти длину образующей \(AB\). В прямоугольном треугольнике \(ABC\) по теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов. Гипотенузой является \(BC\), а катетами — \(AB\) и \(AC\). Поскольку \(AB = AC\), мы можем записать теорему Пифагора как \(AB^2 + AC^2 = BC^2\), что эквивалентно \(AB^2 + AB^2 = 10^2\). Это упрощается до \(2AB^2 = 100\), затем \(AB^2 = 50\). Извлекая квадратный корень, получаем \(AB = \sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2}\) см. Таким образом, длина образующей \(AB\) (и \(AC\)) составляет \(5\sqrt{2}\) см.
Второй шаг — найти радиус основания \(OB\). Хорда \(BC\) является диаметром основания, так как \(\angle BAC = 90^\circ\) и \(BC\) проходит через центр основания \(O\). Следовательно, радиус \(OB\) равен половине диаметра \(BC\). \(OB = \frac{BC}{2} = \frac{10}{2} = 5\) см.
Третий шаг — найти высоту конуса \(AO\). Рассмотрим прямоугольный треугольник \(AOB\), где \(AO\) — высота, \(OB\) — радиус основания, а \(AB\) — образующая. По теореме Пифагора в этом треугольнике \(AO^2 + OB^2 = AB^2\). Подставляем известные значения: \(AO^2 + 5^2 = (5\sqrt{2})^2\). Это дает \(AO^2 + 25 = 50\). Вычитая 25 из обеих сторон, получаем \(AO^2 = 25\). Извлекая квадратный корень, находим высоту \(AO = 5\) см.
Четвертый шаг — вычислить произведение \(AO \cdot OB\). Мы нашли, что \(AO = 5\) см и \(OB = 5\) см. Их произведение равно \(AO \cdot OB = 5 \cdot 5 = 25\) см².
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.