
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 347 Атанасян — Подробные Ответы
Образующая конуса, равная 12 см, наклонена к плоскости основания под углом \(\alpha\). Найдите площадь основания конуса, если: а) \(\alpha = 30^\circ\); б) \(\alpha = 45^\circ\); в) \(\alpha = 60^\circ\).
При \(AB = 12\) см:
а) При \(\angle OBA = 30^\circ\), \(\frac{OB}{AB} = \cos 30^\circ\), следовательно \(\frac{OB}{12} = \frac{\sqrt{3}}{2}\), откуда \(OB = 6\sqrt{3}\). Площадь основания \(S_o = \pi R^2 = \pi (6\sqrt{3})^2 = 108\pi\).
б) При \(\angle OBA = 45^\circ\), \(\frac{OB}{AB} = \cos 45^\circ\), следовательно \(\frac{OB}{12} = \frac{\sqrt{2}}{2}\), откуда \(OB = 6\sqrt{2}\). Площадь основания \(S_o = \pi R^2 = \pi (6\sqrt{2})^2 = 72\pi\).
в) При \(\angle OBA = 60^\circ\), \(\frac{OB}{AB} = \cos 60^\circ\), следовательно \(\frac{OB}{12} = \frac{1}{2}\), откуда \(OB = 6\). Площадь основания \(S_o = \pi R^2 = \pi (6)^2 = 36\pi\).
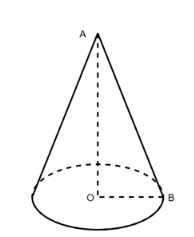
Дано, что длина образующей конуса \(AB = 12\) см. В прямоугольном треугольнике \(OBA\), где \(O\) — центр основания, \(OB\) является радиусом основания \(R\), а \(AB\) — образующей. Угол \(\angle OBA\) дан в каждом из трех случаев.
В случае а) угол \(\angle OBA = 30^\circ\). В прямоугольном треугольнике \(OBA\) косинус угла \(\angle OBA\) равен отношению прилежащего катета \(OB\) к гипотенузе \(AB\), то есть \(\cos(\angle OBA) = \frac{OB}{AB}\). Подставляя известные значения, получаем \(\cos 30^\circ = \frac{OB}{12}\). Значение косинуса 30 градусов равно \(\frac{\sqrt{3}}{2}\). Таким образом, уравнение принимает вид \(\frac{OB}{12} = \frac{\sqrt{3}}{2}\). Решая относительно \(OB\), находим \(OB = 12 \cdot \frac{\sqrt{3}}{2} = 6\sqrt{3}\) см. Радиус основания \(R\) равен \(OB\), следовательно \(R = 6\sqrt{3}\) см. Площадь основания конуса \(S_o\) вычисляется по формуле \(S_o = \pi R^2\). Подставляем значение \(R\): \(S_o = \pi (6\sqrt{3})^2\). Вычисляем \((6\sqrt{3})^2 = 6^2 \cdot (\sqrt{3})^2 = 36 \cdot 3 = 108\). Таким образом, площадь основания \(S_o = 108\pi\) см\(^2\).
В случае б) угол \(\angle OBA = 45^\circ\). Используя ту же тригонометрическую зависимость в прямоугольном треугольнике \(OBA\), имеем \(\cos(\angle OBA) = \frac{OB}{AB}\). Подставляем известные значения: \(\cos 45^\circ = \frac{OB}{12}\). Значение косинуса 45 градусов равно \(\frac{\sqrt{2}}{2}\). Получаем уравнение \(\frac{OB}{12} = \frac{\sqrt{2}}{2}\). Решая относительно \(OB\), находим \(OB = 12 \cdot \frac{\sqrt{2}}{2} = 6\sqrt{2}\) см. Радиус основания \(R\) равен \(OB\), следовательно \(R = 6\sqrt{2}\) см. Площадь основания конуса \(S_o\) вычисляется по формуле \(S_o = \pi R^2\). Подставляем значение \(R\): \(S_o = \pi (6\sqrt{2})^2\). Вычисляем \((6\sqrt{2})^2 = 6^2 \cdot (\sqrt{2})^2 = 36 \cdot 2 = 72\). Таким образом, площадь основания \(S_o = 72\pi\) см\(^2\).
В случае в) угол \(\angle OBA = 60^\circ\). Снова используем тригонометрическую зависимость в прямоугольном треугольнике \(OBA\): \(\cos(\angle OBA) = \frac{OB}{AB}\). Подставляем известные значения: \(\cos 60^\circ = \frac{OB}{12}\). Значение косинуса 60 градусов равно \(\frac{1}{2}\). Получаем уравнение \(\frac{OB}{12} = \frac{1}{2}\). Решая относительно \(OB\), находим \(OB = 12 \cdot \frac{1}{2} = 6\) см. Радиус основания \(R\) равен \(OB\), следовательно \(R = 6\) см. Площадь основания конуса \(S_o\) вычисляется по формуле \(S_o = \pi R^2\). Подставляем значение \(R\): \(S_o = \pi (6)^2\). Вычисляем \((6)^2 = 36\). Таким образом, площадь основания \(S_o = 36\pi\) см\(^2\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!