
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 345 Атанасян — Подробные Ответы
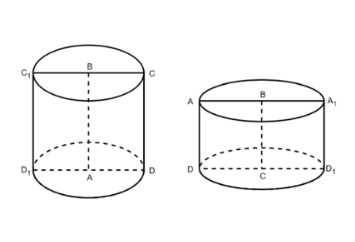
Один цилиндр получен вращением прямоугольника ABCD вокруг прямой AB, а другой цилиндр — вращением этого же прямоугольника вокруг прямой BC. а) Докажите, что площади боковых поверхностей этих цилиндров равны. б) Найдите отношение площадей полных поверхностей этих цилиндров, если AB = a, BC = b.
Площадь боковой поверхности первого цилиндра: \(2\pi \cdot AD \cdot CD\). Площадь боковой поверхности второго цилиндра: \(2\pi \cdot CD \cdot AD\). Очевидно, они равны. Как мы выяснили в предыдущем пункте, площадь боковой поверхности для обоих цилиндров одинакова и равна \(2\pi \cdot AD \cdot CD = 2\pi ab\). Отношение площадей полных поверхностей: \(\frac{S_1}{S_2} = \frac{2\pi ab + 2\pi b^2}{2\pi ab + 2\pi a^2} = \frac{\pi b (a+b)}{\pi a (b+a)} = \frac{b}{a}\).
Решение задачи состоит из двух частей.
В части а) требуется найти площади боковых поверхностей первого и второго цилиндров и сравнить их. Площадь боковой поверхности цилиндра вычисляется по формуле \(2\pi r h\), где \(r\) — радиус основания, а \(h\) — высота цилиндра. Для первого цилиндра радиус основания равен \(AD\), а высота — \(CD\). Следовательно, площадь его боковой поверхности равна \(2\pi \cdot AD \cdot CD\). Для второго цилиндра радиус основания равен \(CD\), а высота — \(AD\). Следовательно, площадь его боковой поверхности равна \(2\pi \cdot CD \cdot AD\). Поскольку умножение коммутативно, \(AD \cdot CD = CD \cdot AD\), отсюда следует, что \(2\pi \cdot AD \cdot CD = 2\pi \cdot CD \cdot AD\). Таким образом, площади боковых поверхностей первого и второго цилиндров равны.
В части б) требуется найти отношение полных площадей поверхностей этих цилиндров. Как было установлено в части а), площадь боковой поверхности для обоих цилиндров одинакова и равна \(2\pi \cdot AD \cdot CD\). Обозначим \(AD = a\) и \(CD = b\). Тогда площадь боковой поверхности равна \(2\pi ab\). Полная площадь поверхности цилиндра складывается из площади боковой поверхности и площадей двух оснований. Площадь основания круга равна \(\pi r^2\). Для расчета отношения полных площадей поверхностей, обозначенных как \(S_1\) и \(S_2\), используются формулы \(S_1 = 2\pi ab + 2\pi b^2\) и \(S_2 = 2\pi ab + 2\pi a^2\). Заметим, что формула для \(S_1\) соответствует цилиндру с радиусом \(b\) и высотой \(a\) (боковая поверхность \(2\pi b a = 2\pi ab\), площади оснований \(2 \cdot \pi b^2 = 2\pi b^2\)), а формула для \(S_2\) соответствует цилиндру с радиусом \(a\) и высотой \(b\) (боковая поверхность \(2\pi a b\), площади оснований \(2 \cdot \pi a^2 = 2\pi a^2\)). Найдем отношение \(S_1\) к \(S_2\): \(\frac{S_1}{S_2} = \frac{2\pi ab + 2\pi b^2}{2\pi ab + 2\pi a^2}\). Вынесем общие множители в числителе и знаменателе. В числителе можно вынести \(2\pi b\), получим \(2\pi b (a+b)\). В знаменателе можно вынести \(2\pi a\), получим \(2\pi a (b+a)\). Тогда отношение примет вид: \(\frac{S_1}{S_2} = \frac{2\pi b (a+b)}{2\pi a (b+a)}\). Поскольку \(a+b = b+a\), мы можем сократить члены \(2\pi\) и \((a+b)\) в числителе и знаменателе. В результате получаем: \(\frac{S_1}{S_2} = \frac{b}{a}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!