Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 342 Атанасян — Подробные Ответы
Угол между диагоналями развёртки боковой поверхности цилиндра равен \(\phi\), диагональ равна d. Найдите площади боковой и полной поверхностей цилиндра.
Боковая поверхность цилиндра представляет собой прямоугольник со сторонами \(CD = d \sqrt{\frac{1 — \cos \phi}{2}}\) и \(BC = d \sqrt{\frac{1 + \cos \phi}{2}}\) при условии, что угол между диагоналями \(\angle DOC = \phi\). Площадь боковой поверхности равна произведению этих сторон, что дает \(d^2 \frac{\sin \phi}{2}\).
Грань BC является окружностью основания, поэтому \(BC = 2\pi R\). Из этого следует, что радиус основания \(R = \frac{BC}{2\pi}\).
Если \(\angle DOC = \phi\), то \(BC = d \sqrt{\frac{1 + \cos \phi}{2}}\), и площадь оснований \(S_o = 2\pi R^2 = 2\pi \left( \frac{d \sqrt{\frac{1 + \cos \phi}{2}}}{2\pi} \right)^2 = \frac{d^2 \cos^2 \frac{\phi}{2}}{2\pi}\). Полная площадь поверхности в этом случае равна \(d^2 \frac{\sin \phi}{2} + \frac{d^2 \cos^2 \frac{\phi}{2}}{2\pi}\).
Если выбрать угол иначе, например \(\angle COB = \phi\), то \(BC = d \sqrt{\frac{1 — \cos \phi}{2}}\), и площадь оснований \(S_o = 2\pi R^2 = 2\pi \left( \frac{d \sqrt{\frac{1 — \cos \phi}{2}}}{2\pi} \right)^2 = \frac{d^2 \sin^2 \frac{\phi}{2}}{2\pi}\). Полная площадь поверхности в этом случае равна \(d^2 \frac{\sin \phi}{2} + \frac{d^2 \sin^2 \frac{\phi}{2}}{2\pi}\).
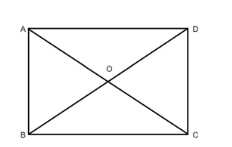
Боковая поверхность цилиндра при развертке представляет собой прямоугольник. Диагонали этого прямоугольника пересекаются и делятся точкой пересечения пополам. Пусть длина каждой диагонали прямоугольника равна \(d\). Тогда отрезки диагоналей от центра до вершин равны \(d/2\).
Для определенности рассмотрим треугольник, образованный двумя половинками диагоналей и одной из сторон прямоугольника. Пусть угол между половинками диагоналей равен \(\phi\). По теореме косинусов, квадрат длины стороны прямоугольника (например, CD) равен сумме квадратов длин половинок диагоналей минус удвоенное произведение этих длин на косинус угла между ними:
\(CD^2 = \left(\frac{d}{2}\right)^2 + \left(\frac{d}{2}\right)^2 — 2 \left(\frac{d}{2}\right) \left(\frac{d}{2}\right) \cos \phi\)
\(CD^2 = \frac{d^2}{4} + \frac{d^2}{4} — 2 \frac{d^2}{4} \cos \phi\)
\(CD^2 = \frac{d^2}{2} — \frac{d^2}{2} \cos \phi\)
\(CD^2 = \frac{d^2}{2} (1 — \cos \phi)\)
\(CD = \sqrt{\frac{d^2}{2} (1 — \cos \phi)} = d \sqrt{\frac{1 — \cos \phi}{2}}\)
Смежный угол между диагоналями равен \(180^\circ — \phi\). Для другой стороны прямоугольника (например, BC) используем этот угол:
\(BC^2 = \left(\frac{d}{2}\right)^2 + \left(\frac{d}{2}\right)^2 — 2 \left(\frac{d}{2}\right) \left(\frac{d}{2}\right) \cos (180^\circ — \phi)\)
Поскольку \(\cos (180^\circ — \phi) = -\cos \phi\), получаем:
\(BC^2 = \frac{d^2}{4} + \frac{d^2}{4} — 2 \frac{d^2}{4} (-\cos \phi)\)
\(BC^2 = \frac{d^2}{2} + \frac{d^2}{2} \cos \phi\)
\(BC^2 = \frac{d^2}{2} (1 + \cos \phi)\)
\(BC = \sqrt{\frac{d^2}{2} (1 + \cos \phi)} = d \sqrt{\frac{1 + \cos \phi}{2}}\)
Площадь боковой поверхности прямоугольника равна произведению его сторон BC и CD:
\(Area_{lateral} = BC \times CD = \left(d \sqrt{\frac{1 + \cos \phi}{2}}\right) \left(d \sqrt{\frac{1 — \cos \phi}{2}}\right)\)
\(Area_{lateral} = d^2 \sqrt{\frac{(1 + \cos \phi)(1 — \cos \phi)}{4}}\)
\(Area_{lateral} = d^2 \sqrt{\frac{1 — \cos^2 \phi}{4}}\)
\(Area_{lateral} = d^2 \sqrt{\frac{\sin^2 \phi}{4}}\)
\(Area_{lateral} = d^2 \frac{|\sin \phi|}{2}\). Поскольку \(\phi\) является углом между диагоналями прямоугольника, \(0 < \phi < 180^\circ\), и \(\sin \phi > 0\).
\(Area_{lateral} = d^2 \frac{\sin \phi}{2}\)
Одна из сторон прямоугольника (например, BC) является длиной окружности основания цилиндра, то есть \(BC = 2\pi R\), где \(R\) — радиус основания.
Если мы предположили, что угол между диагоналями, соответствующий стороне CD, равен \(\phi\), тогда угол, соответствующий стороне BC, равен \(180^\circ — \phi\), и \(BC = d \sqrt{\frac{1 + \cos \phi}{2}}\).
Тогда радиус основания \(R = \frac{BC}{2\pi} = \frac{d \sqrt{\frac{1 + \cos \phi}{2}}}{2\pi} = \frac{d}{2\pi} \sqrt{\frac{1 + \cos \phi}{2}}\).
Площадь двух оснований \(S_o = 2 \times (\pi R^2) = 2\pi \left(\frac{d}{2\pi} \sqrt{\frac{1 + \cos \phi}{2}}\right)^2\)
\(S_o = 2\pi \frac{d^2}{(2\pi)^2} \frac{1 + \cos \phi}{2}\)
\(S_o = 2\pi \frac{d^2}{4\pi^2} \frac{1 + \cos \phi}{2}\)
\(S_o = \frac{d^2}{2\pi} \frac{1 + \cos \phi}{2}\)
Используя формулу половинного угла \(\cos^2 \frac{\phi}{2} = \frac{1 + \cos \phi}{2}\), получаем:
\(S_o = \frac{d^2}{2\pi} \cos^2 \frac{\phi}{2}\)
Полная площадь поверхности в этом случае равна сумме площади боковой поверхности и площади двух оснований:
\(Area_{total, 1} = Area_{lateral} + S_o = d^2 \frac{\sin \phi}{2} + \frac{d^2 \cos^2 \frac{\phi}{2}}{2\pi}\)
Если выбрать угол \(\phi\) иначе, подразумевая, что угол между диагоналями, соответствующий стороне BC, равен \(\phi\), тогда \(BC = d \sqrt{\frac{1 — \cos \phi}{2}}\).
Радиус основания в этом случае \(R = \frac{BC}{2\pi} = \frac{d \sqrt{\frac{1 — \cos \phi}{2}}}{2\pi} = \frac{d}{2\pi} \sqrt{\frac{1 — \cos \phi}{2}}\).
Площадь двух оснований \(S_o = 2 \times (\pi R^2) = 2\pi \left(\frac{d}{2\pi} \sqrt{\frac{1 — \cos \phi}{2}}\right)^2\)
\(S_o = 2\pi \frac{d^2}{(2\pi)^2} \frac{1 — \cos \phi}{2}\)
\(S_o = \frac{d^2}{2\pi} \frac{1 — \cos \phi}{2}\)
Используя формулу половинного угла \(\sin^2 \frac{\phi}{2} = \frac{1 — \cos \phi}{2}\), получаем:
\(S_o = \frac{d^2}{2\pi} \sin^2 \frac{\phi}{2}\)
Площадь боковой поверхности остается прежней, \(d^2 \frac{\sin \phi}{2}\), так как она зависит от произведения сторон, а не от того, какой угол мы назвали \(\phi\).
Полная площадь поверхности во втором случае равна:
\(Area_{total, 2} = Area_{lateral} + S_o = d^2 \frac{\sin \phi}{2} + \frac{d^2 \sin^2 \frac{\phi}{2}}{2\pi}\)
Таким образом, получаем два варианта площади полной поверхности в зависимости от того, какой из смежных углов между диагоналями прямоугольника принят за \(\phi\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.