ГДЗ по Геометрии 10 класс Номер 335 Атанасян — Подробные Ответы

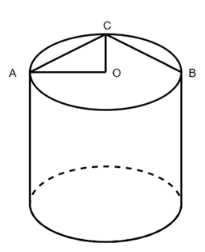
Через образующую цилиндра проведены две взаимно перпендикулярные плоскости. Площадь каждого из полученных сечений равна S. Найдите площадь осевого сечения цилиндра.

Площадь сечения равна произведению высоты на длину хорды основания. Для равных площадей сечений длины хорд должны быть равны. Для взаимно перпендикулярных сечений с равными площадями хорды АС и ВС имеют длину \(l\). Радиус основания цилиндра \(R\). Если угол АОС прямой, то \(R = \frac{l}{\sqrt{2}}\). Площадь осевого сечения \(S_c = 2hR = lh\sqrt{2}\). Площадь взаимно перпендикулярных сечений \(S = hl\). Отношение площадей \(\frac{S_o}{S} = \frac{lh\sqrt{2}}{lh} = \sqrt{2}\), откуда \(S_o = S\sqrt{2}\).

Площадь любого сечения цилиндра, проходящего через его высоту, определяется как произведение высоты цилиндра на длину хорды основания, которую это сечение образует. Если площади двух таких сечений равны, то и длины соответствующих хорд на основании цилиндра должны быть равны, поскольку высота цилиндра для обоих сечений одна и та же. В случае двух взаимно перпендикулярных сечений с равными площадями, хорды, лежащие в основании, также взаимно перпендикулярны и имеют равные длины. Обозначим длину каждой из этих равных хорд как \(l\). Пусть О — центр основания цилиндра, а А и С — концы одной из таких хорд. Тогда ОА и ОС являются радиусами основания цилиндра, обозначим их \(R\). Если хорды взаимно перпендикулярны и имеют равную длину, то угол между радиусами, проведенными к концам одной из хорд, может быть прямым. В данном случае, если угол АОС прямой, то треугольник АОС является прямоугольным и равнобедренным с катетами ОА = ОС = \(R\) и гипотенузой АС = \(l\). По теореме Пифагора имеем \(R^2 + R^2 = l^2\), что упрощается до \(2R^2 = l^2\). Из этого следует, что \(R\sqrt{2} = l\), и радиус основания выражается через длину хорды как \(R = \frac{l}{\sqrt{2}}\).

Теперь рассмотрим площадь осевого сечения. Осевое сечение — это сечение, проходящее через ось цилиндра. Оно представляет собой прямоугольник, одна сторона которого равна высоте цилиндра \(h\), а другая сторона равна диаметру основания, то есть \(2R\). Площадь осевого сечения \(S_c\) равна произведению высоты на диаметр: \(S_c = h \times (2R)\). Подставляя выражение для \(R\) через \(l\), получаем \(S_c = h \times 2 \times \frac{l}{\sqrt{2}} = hl\sqrt{2}\).

Площадь одного из взаимно перпендикулярных сечений, проходящего через хорду длиной \(l\), равна произведению высоты цилиндра \(h\) на длину этой хорды \(l\). Обозначим площадь такого сечения как \(S\). Тогда \(S = hl\).

Теперь найдем отношение площади осевого сечения к площади одного из взаимно перпендикулярных сечений. В примере это отношение обозначено как \(\frac{S_o}{S}\), где \(S_o\) соответствует площади осевого сечения \(S_c\), а \(S\) — площади взаимно перпендикулярного сечения.
\(\frac{S_o}{S} = \frac{S_c}{S} = \frac{lh\sqrt{2}}{lh}\).
Сокращая \(lh\) в числителе и знаменателе, получаем \(\frac{S_o}{S} = \sqrt{2}\).
Из этого соотношения следует, что площадь осевого сечения \(S_o\) в \(\sqrt{2}\) раз больше площади взаимно перпендикулярного сечения \(S\), то есть \(S_o = S\sqrt{2}\).