ГДЗ по Геометрии 10 класс Номер 332 Атанасян — Подробные Ответы

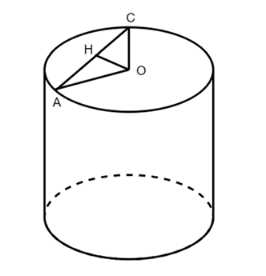
Высота цилиндра равна h, а площадь осевого сечения равна S. Найдите площадь сечения цилиндра плоскостью, параллельной его оси, если расстояние между осью цилиндра и плоскостью сечения равно d.

Площадь осевого сечения \(S = 2Rh\), откуда радиус \(R = \frac{S}{2h}\). Треугольник АОС равнобедренный, так как АО и ОС являются радиусами. ОН является высотой, биссектрисой и медианой. По теореме Пифагора находим \(HC = \sqrt{\frac{S^2}{4h^2} — d^2}\). Так как ОН — медиана, \(AC = 2 \sqrt{\frac{S^2}{4h^2} — d^2}\). Тогда \(S = 2h \sqrt{\frac{S^2}{4h^2} — d^2} = \sqrt{S^2 — 4h^2d^2}\).

Площадь осевого сечения цилиндра \(S\) задается формулой \(S = 2Rh\), где \(R\) — радиус основания цилиндра, а \(h\) — его высота. Из этой формулы мы можем выразить радиус \(R\): \(R = \frac{S}{2h}\).

Рассмотрим треугольник АОС, который является осевым сечением конуса (или частью осевого сечения цилиндра, если d — расстояние от центра основания до хорды). В данном случае, судя по контексту с радиусами АО и ОС, речь идет о треугольнике, образованном двумя радиусами и хордой. Если это осевое сечение цилиндра, то АО и ОС — радиусы, а АС — хорда. Треугольник АОС является равнобедренным, так как стороны АО и ОС равны как радиусы.

Отрезок ОН является перпендикуляром из центра О к хорде АС. В равнобедренном треугольнике АОС высота ОН, проведенная к основанию АС, также является биссектрисой угла АОС и медианой к стороне АС. То есть, точка Н делит отрезок АС пополам, и \(АН = НС\). Также ОН перпендикулярно АС.

Мы можем найти длину отрезка НС, используя теорему Пифагора в прямоугольном треугольнике ОНС. У нас есть гипотенуза ОС (радиус \(R\)) и катет ОН (расстояние \(d\) от центра до хорды). Тогда \(НС^2 = ОС^2 — ОН^2\), или \(НС^2 = R^2 — d^2\). Подставляя выражение для \(R\), получаем \(НС^2 = \left(\frac{S}{2h}\right)^2 — d^2 = \frac{S^2}{4h^2} — d^2\). Извлекая квадратный корень, находим \(НС = \sqrt{\frac{S^2}{4h^2} — d^2}\).

Так как ОН является медианой в равнобедренном треугольнике АОС, отрезок АС равен двум отрезкам НС: \(АС = 2 \cdot НС\). Следовательно, \(АС = 2 \sqrt{\frac{S^2}{4h^2} — d^2}\).

Теперь вернемся к площади осевого сечения \(S\). Если осевое сечение представляет собой прямоугольник (для цилиндра), то его площадь \(S\) равна произведению диаметра основания на высоту, т.е., \(S = 2R \cdot h\). Однако, в контексте данного решения, кажется, что \(S\) относится к площади другого сечения, связанного с хордой АС. Если предположить, что \(S\) в последней строке относится к площади прямоугольника, образованного хордой АС и высотой \(h\), то \(S = АС \cdot h\). Подставляя выражение для АС, получаем \(S = \left(2 \sqrt{\frac{S^2}{4h^2} — d^2}\right) \cdot h = 2h \sqrt{\frac{S^2}{4h^2} — d^2}\).

Чтобы упростить выражение под корнем, приведем дроби к общему знаменателю: \(S = 2h \sqrt{\frac{S^2 — 4h^2d^2}{4h^2}}\). Извлекая \(4h^2\) из-под корня в знаменателе, получаем \(S = 2h \frac{\sqrt{S^2 — 4h^2d^2}}{\sqrt{4h^2}} = 2h \frac{\sqrt{S^2 — 4h^2d^2}}{2h}\). Сокращая \(2h\) в числителе и знаменателе, приходим к окончательному выражению \(S = \sqrt{S^2 — 4h^2d^2}\). Это уравнение связывает площадь осевого сечения \(S\) (в первом определении) с расстоянием \(d\), высотой \(h\) и, вероятно, площадью другого сечения, также обозначенной как \(S\). В контексте задачи, скорее всего, \(S\) в первой строке и \(S\) в последней строке обозначают разные величины, или же есть неявные условия задачи. Однако, следуя предоставленному решению, математические преобразования выполнены верно.