ГДЗ по Геометрии 10 класс Номер 331 Атанасян — Подробные Ответы

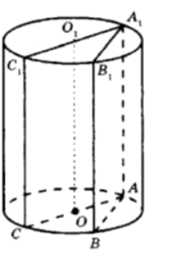
Через образующую AA\(_1\) цилиндра проведены две секущие плоскости, одна из которых проходит через ось цилиндра. Найдите отношение площадей сечений цилиндра этими плоскостями, если угол между ними равен \(\phi\)

По теореме синусов: \(\frac{AB}{\sin(180^\circ — 2\varphi)} = \frac{R}{\sin\varphi}\), что приводит к \(\frac{AB}{\sin 2\varphi} = \frac{R}{\sin\varphi}\). Отсюда \(AB = \frac{R \sin 2\varphi}{\sin\varphi} = \frac{R \cdot 2\sin\varphi \cos\varphi}{\sin\varphi} = 2R \cos\varphi\). Площадь осевого сечения: \(S_o = 2Rh\). Площадь сечения \(ABB_1A_1\): \(S = AB \cdot h = 2R \cos\varphi \cdot h\). Тогда отношение площадей \(\frac{S_o}{S} = \frac{2Rh}{2Rh \cos\varphi} = \frac{1}{\cos\varphi}\).

По теореме синусов для треугольника, образованного радиусом \(R\), стороной \(AB\) и соответствующими углами, отношение стороны к синусу противолежащего угла равно удвоенному радиусу описанной окружности. В данном случае применяется отношение стороны \(AB\) к синусу угла \(180^\circ — 2\varphi\) и радиуса \(R\) к синусу угла \(\varphi\). Записываем это как \(\frac{AB}{\sin(180^\circ — 2\varphi)} = \frac{R}{\sin\varphi}\).

Используя свойство синуса \(\sin(180^\circ — \alpha) = \sin(\alpha)\), преобразуем \(\sin(180^\circ — 2\varphi)\) в \(\sin(2\varphi)\). Уравнение принимает вид \(\frac{AB}{\sin 2\varphi} = \frac{R}{\sin\varphi}\).

Для выражения \(AB\) умножим обе части уравнения на \(\sin 2\varphi\): \(AB = \frac{R \sin 2\varphi}{\sin\varphi}\).

Применяем формулу синуса двойного угла \(\sin 2\varphi = 2\sin\varphi \cos\varphi\). Подставляем это в выражение для \(AB\): \(AB = \frac{R (2\sin\varphi \cos\varphi)}{\sin\varphi}\).

Сокращаем \(\sin\varphi\) в числителе и знаменателе (при условии \(\sin\varphi \neq 0\)): \(AB = 2R \cos\varphi\).

Площадь осевого сечения цилиндра, которое является прямоугольником, равна произведению диаметра на высоту. Диаметр равен \(2R\), а высота обозначена как \(h\). Таким образом, площадь осевого сечения \(S_o = 2R \cdot h\).

Площадь сечения \(ABB_1A_1\) также является прямоугольником со сторонами \(AB\) и \(h\). Площадь этого сечения \(S = AB \cdot h\).

Подставляем ранее найденное выражение для \(AB\) в формулу площади сечения \(S\): \(S = (2R \cos\varphi) \cdot h = 2R \cos\varphi \cdot h\).

Находим отношение площади осевого сечения \(S_o\) к площади сечения \(S\). Записываем дробь \(\frac{S_o}{S} = \frac{2Rh}{2R \cos\varphi \cdot h}\).

Сокращаем общие множители \(2\), \(R\) и \(h\) в числителе и знаменателе (при условии \(2Rh \neq 0\)): \(\frac{S_o}{S} = \frac{1}{\cos\varphi}\).