Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 330 Атанасян — Подробные Ответы
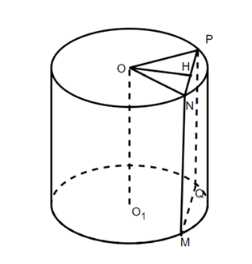
Высота цилиндра равна 10 дм. Площадь сечения цилиндра плоскостью, параллельной оси цилиндра и удалённой на 9 дм от неё, равна 240 дм\(^2\). Найдите радиус цилиндра.
\(PN = \frac{S_{PNMQ}}{PQ} = \frac{240}{10} = 24\) см.
PON — равнобедренный треугольник, соответственно OH — медиана, высота и биссектриса одновременно.
Тогда \(R = OP = \sqrt{OH^2 + PH^2} = \sqrt{225} = 15\) см.
Из условия задачи и предоставленного рисунка видно, что PNMQ является прямоугольником, вписанным в цилиндр. Площадь этого прямоугольника \(S_{PNMQ}\) равна 240, а одна из его сторон, PQ, равна 10 см. Сторона PN является другой стороной этого прямоугольника. Площадь прямоугольника равна произведению его сторон, то есть \(S_{PNMQ} = PN \cdot PQ\). Подставляя известные значения, получаем \(240 = PN \cdot 10\). Чтобы найти длину стороны PN, необходимо разделить площадь на известную сторону: \(PN = \frac{240}{10} = 24\) см.
Далее рассматривается треугольник PON. Из рисунка и текста следует, что этот треугольник является равнобедренным с вершиной O в центре верхнего основания цилиндра и основанием PN, лежащим на хорде верхнего основания. Отрезок OH является высотой этого равнобедренного треугольника, опущенной из вершины O на основание PN. В равнобедренном треугольнике высота, проведенная к основанию, также является медианой и биссектрисой. Точка H является серединой отрезка PN.
Теперь рассмотрим прямоугольный треугольник OHP. OP является радиусом верхнего основания цилиндра, который мы обозначим как R. OH — это расстояние от центра верхнего основания до хорды PN. PH — это половина длины отрезка PN, так как H — середина PN. Мы нашли, что \(PN = 24\) см, следовательно, \(PH = \frac{PN}{2} = \frac{24}{2} = 12\) см. В прямоугольном треугольнике OHP по теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов: \(OP^2 = OH^2 + PH^2\). Из предоставленного решения видно, что \(R = OP = \sqrt{OH^2 + PH^2} = \sqrt{225}\). Вычисляя квадратный корень из 225, получаем \(R = 15\) см. Таким образом, радиус основания цилиндра равен 15 см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.