
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 33 Атанасян — Подробные Ответы
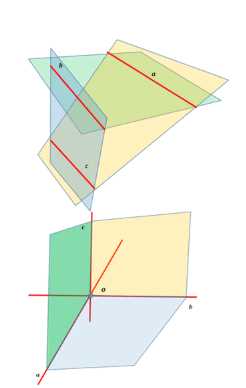
Докажите, что если три плоскости, не проходящие через одну прямую, попарно пересекаются, то прямые, по которым они пересекаются, либо параллельны, либо имеют общую точку.
Дано: три плоскости \(\alpha\), \(\beta\), \(\gamma\), которые не проходят через одну прямую, попарно пересекаются, образуя прямые \(a = \alpha \cap \beta\), \(b = \beta \cap \gamma\), \(c = \gamma \cap \alpha\).
Если прямые \(a\), \(b\), \(c\) имеют общую точку, то эта точка принадлежит всем трём плоскостям, и прямые пересекаются в одной точке.
Если \(a \cap b = \emptyset\), то \(a\) и \(b\) лежат в плоскости \(\beta\) и параллельны, так как не пересекаются. Аналогично для пар \(b\) и \(c\), \(c\) и \(a\).
Следовательно, прямые \(a\), \(b\), \(c\) либо параллельны, либо имеют общую точку.
Дано: три плоскости \(\alpha\), \(\beta\), \(\gamma\), которые не проходят через одну прямую, попарно пересекаются, образуя прямые \(a = \alpha \cap \beta\), \(b = \beta \cap \gamma\), \(c = \gamma \cap \alpha\). Требуется доказать, что прямые \(a\), \(b\), \(c\) либо параллельны, либо имеют общую точку.
Рассмотрим пересечения каждой пары плоскостей. Поскольку плоскости \(\alpha\), \(\beta\), \(\gamma\) не проходят через одну прямую, их попарные пересечения дают три различные прямые \(a\), \(b\), \(c\).
Пусть \(a \cap b = P\). Тогда точка \(P\) принадлежит одновременно плоскостям \(\alpha\), \(\beta\), \(\gamma\). Если \(P\) существует, то все три прямые \(a\), \(b\), \(c\) пересекаются в одной точке \(P\), что соответствует утверждению задачи.
Если \(a \cap b = \emptyset\), то прямые \(a\) и \(b\) не пересекаются. В этом случае они лежат в одной плоскости \(\beta\), так как \(a \subset \beta\) и \(b \subset \beta\). Следовательно, \(a \parallel b\).
Аналогично для других пар прямых \(b\) и \(c\), \(c\) и \(a\): если они не пересекаются, то они параллельны, так как находятся в одной из плоскостей \(\gamma\) или \(\alpha\).
Таким образом, прямые \(a\), \(b\), \(c\) либо пересекаются в одной точке, либо попарно параллельны. Это и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!