ГДЗ по Геометрии 10 класс Номер 329 Атанасян — Подробные Ответы

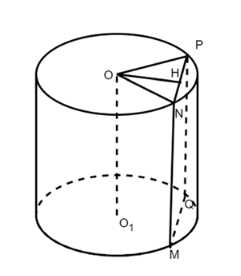
Высота цилиндра равна 12 см, а радиус основания равен 10 см. Цилиндр пересечён плоскостью, параллельной его оси, так, что в сечении получился квадрат. Найдите расстояние от оси цилиндра до секущей плоскости.

Треугольник PON является равнобедренным, следовательно OH — медиана, высота и биссектриса одновременно. OP — радиус основания. Тогда, по теореме Пифагора: \(OH = \sqrt{OP^2 — HP^2} = \sqrt{100 — 36} = \sqrt{64} = 8\) см.

В данном решении рассматривается треугольник PON, который по условию является равнобедренным. Из того, что треугольник PON равнобедренный, следует, что высота OH, проведенная к основанию PN, также является медианой и биссектрисой этого треугольника. Отрезок OP представляет собой радиус основания цилиндра. Для того чтобы найти длину отрезка OH, мы можем воспользоваться теоремой Пифагора в прямоугольном треугольнике OHP. В этом треугольнике OP является гипотенузой, а OH и HP являются катетами. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, то есть \(OP^2 = OH^2 + HP^2\). Из этой формулы мы можем выразить квадрат катета OH: \(OH^2 = OP^2 — HP^2\). Чтобы найти саму длину OH, необходимо извлечь квадратный корень из разности квадратов OP и HP: \(OH = \sqrt{OP^2 — HP^2}\). Подставляя числовые значения из примера, где \(OP^2\) равно 100 и \(HP^2\) равно 36, получаем: \(OH = \sqrt{100 — 36}\). Вычисляем разность под корнем: \(100 — 36 = 64\). Таким образом, \(OH = \sqrt{64}\). Извлекая квадратный корень из 64, получаем 8. Следовательно, длина отрезка OH составляет 8 см. Таким образом, по теореме Пифагора найдена длина отрезка OH.