
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 327 Атанасян — Подробные Ответы
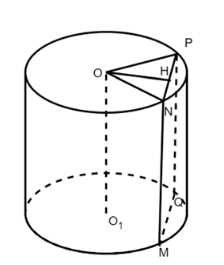
Докажите, что если секущая плоскость параллельна оси цилиндра и расстояние между этой плоскостью и осью цилиндра меньше его радиуса, то сечение цилиндра представляет собой прямоугольник, две противоположные стороны которого — образующие цилиндра.
Известно, что секущая плоскость параллельна оси цилиндра. Ось перпендикулярна плоскости основания, соответственно, секущая плоскость также ей перпендикулярна. Тогда прямые NM и PQ, по которым секущая плоскость пересекает боковую поверхность цилиндра, тоже перпендикулярны плоскостям основания. Соответственно PQMN — прямоугольник. Что и требовалось доказать.
Известно, что секущая плоскость параллельна оси цилиндра. Это означает, что плоскость расположена таким образом, что она не пересекает ось цилиндра и сохраняет постоянное расстояние от нее.
Ось цилиндра перпендикулярна плоскости основания. Это фундаментальное свойство прямого цилиндра. Ось проходит через центры обоих оснований и перпендикулярна им.
Соответственно, секущая плоскость также перпендикулярна плоскости основания. Поскольку секущая плоскость параллельна оси, а ось перпендикулярна основанию, то и секущая плоскость, будучи «параллельной направлению перпендикуляра», сама становится перпендикулярной к этой плоскости основания.
Тогда прямые NM и PQ, по которым секущая плоскость пересекает боковую поверхность цилиндра, тоже перпендикулярны плоскостям основания. Боковая поверхность цилиндра состоит из образующих, которые параллельны оси и, следовательно, перпендикулярны основаниям. Секущая плоскость, будучи перпендикулярной основаниям, пересекает эти образующие. Линии пересечения NM и PQ являются частями этих образующих, ограниченными секущей плоскостью и основаниями (или воображаемыми плоскостями оснований, если плоскость пересекает только боковую поверхность). Поскольку образующие перпендикулярны основаниям, то и отрезки NM и PQ, лежащие на этих образующих, перпендикулярны основаниям.
Соответственно PQMN — прямоугольник. Фигура PQMN образована двумя параллельными и перпендикулярными основаниям отрезками NM и PQ, и отрезками NP и MQ, лежащими в плоскостях оснований. Поскольку NM и PQ перпендикулярны плоскостям оснований, они перпендикулярны любым прямым в этих плоскостях, проходящим через их концы, в частности, NP и MQ. Так как NM и PQ являются отрезками образующих, они параллельны и равны по длине. Отрезки NP и MQ соединяют соответствующие точки на окружностях оснований, лежащие в секущей плоскости. В силу параллельности секущей плоскости оси и ее перпендикулярности основаниям, сечение является прямоугольником. Стороны NM и PQ перпендикулярны сторонам NP и MQ.
Что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!