
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 326 Атанасян — Подробные Ответы
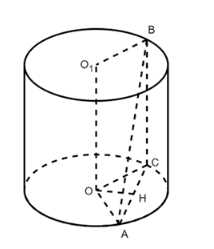
Концы отрезка AB лежат на окружностях оснований цилиндра. Радиус цилиндра равен r, его высота — h, а расстояние между прямой AB и осью цилиндра равно d. Найдите: а) h, если r = 10 дм, d = 8 дм, AB = 13 дм; б) d, если h = 6 см, r = 5 см, AB = 10 см.
СОА — равнобедренный треугольник, соответственно ОН — медиана, высота и бисектрисса одновременно.
а) ОС — радиус основания. Тогда, по теореме Пифагора:
\(CH = \sqrt{OC^2 — OH^2} = \sqrt{100 — 64} = 6 \text{ см} \rightarrow AC = 2CH = 12 \text{ см}\)
Треугольник АВС прямоугольный, ВС — высота цилиндра. По теореме Пифагора:
\(BC = \sqrt{AB^2 — AC^2} = \sqrt{169 — 144} = 5 \text{ см}\)
б) По теореме Пифагора:
\(AC = \sqrt{AB^2 — BC^2} = \sqrt{100 — 36} = 8 \text{ см}.\)
Так как ОН – медиана, \(CH = \frac{AC}{2} = 4 \text{ см}.\)
Тогда, по теореме Пифагора:
\(OH = \sqrt{OC^2 — CH^2} = \sqrt{25 — 16} = 3 \text{ см}\)
СОА является равнобедренным треугольником, из чего следует, что ОН, будучи медианой, одновременно является высотой и биссектрисой.
а) Поскольку ОС является радиусом основания, мы можем использовать теорему Пифагора для нахождения длины отрезка CH в прямоугольном треугольнике COH. По условию, \(OC^2 = 100\) и \(OH^2 = 64\).
Применяя теорему Пифагора \(c^2 = a^2 + b^2\), где \(c\) — гипотенуза, а \(a\) и \(b\) — катеты, получаем:
\(OC^2 = CH^2 + OH^2\)
\(100 = CH^2 + 64\)
\(CH^2 = 100 — 64\)
\(CH^2 = 36\)
Извлекая квадратный корень, находим длину CH:
\(CH = \sqrt{36} = 6 \text{ см}\)
Так как ОН является медианой в равнобедренном треугольнике СОА, она делит основание АС пополам. Следовательно, длина АС в два раза больше длины CH:
\(AC = 2 \cdot CH = 2 \cdot 6 = 12 \text{ см}\)
Треугольник АВС является прямоугольным, и ВС представляет собой высоту цилиндра. Для нахождения длины ВС мы снова применим теорему Пифагора в прямоугольном треугольнике АВС. По условию, \(AB^2 = 169\) и \(AC^2 = 144\).
Применяя теорему Пифагора:
\(AB^2 = AC^2 + BC^2\)
\(169 = 144 + BC^2\)
\(BC^2 = 169 — 144\)
\(BC^2 = 25\)
Извлекая квадратный корень, находим длину ВС:
\(BC = \sqrt{25} = 5 \text{ см}\)
б) В этом случае, для нахождения длины АС, мы используем теорему Пифагора в прямоугольном треугольнике АВС, где \(AB^2 = 100\) и \(BC^2 = 36\).
Применяя теорему Пифагора:
\(AB^2 = AC^2 + BC^2\)
\(100 = AC^2 + 36\)
\(AC^2 = 100 — 36\)
\(AC^2 = 64\)
Извлекая квадратный корень, находим длину АС:
\(AC = \sqrt{64} = 8 \text{ см}.\)
Поскольку ОН является медианой в равнобедренном треугольнике СОА, она делит основание АС пополам. Следовательно, длина CH равна половине длины АС:
\(CH = \frac{AC}{2} = \frac{8}{2} = 4 \text{ см}.\)
Теперь, для нахождения длины ОН, мы применим теорему Пифагора в прямоугольном треугольнике COH. По условию, \(OC^2 = 25\) и мы только что нашли \(CH^2 = 4^2 = 16\).
Применяя теорему Пифагора:
\(OC^2 = CH^2 + OH^2\)
\(25 = 16 + OH^2\)
\(OH^2 = 25 — 16\)
\(OH^2 = 9\)
Извлекая квадратный корень, находим длину ОН:
\(OH = \sqrt{9} = 3 \text{ см}\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!