Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 325 Атанасян — Подробные Ответы
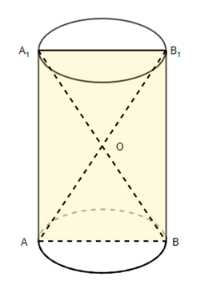
Площадь основания цилиндра относится к площади осевого сечения как \(\sqrt{3}\pi : 4\). Найдите: а) угол между диагональю осевого сечения цилиндра и плоскостью основания; б) угол между диагоналями осевого сечения.
Обозначим площадь основания \(S\), площадь сечения \(S_c\).
\(\frac{S}{S_c} = \frac{\sqrt{3}\pi}{4} \rightarrow \frac{\pi R^2}{AB \cdot BB_1} = \frac{\sqrt{3}\pi}{4} \rightarrow \frac{R}{BB_1} = \frac{\sqrt{3}}{2}\)
\(\text{ctg}\angle B_1 AB = \sqrt{3} \rightarrow \angle B_1 AB = 30^\circ\)
\(\angle OAB = \angle OBA \rightarrow \angle BOA = 180^\circ — 2 \cdot 30^\circ = 120^\circ\)
Обозначим площадь основания цилиндра как \(S\), а площадь осевого сечения \(AB_1 A_1 B\) как \(S_c\). Площадь основания цилиндра с радиусом \(R\) равна \(S = \pi R^2\). Осевое сечение \(AB_1 A_1 B\) является прямоугольником, где \(AB\) — диаметр основания, и \(BB_1\) — высота цилиндра. Длина диаметра \(AB = 2R\). Площадь прямоугольного сечения \(S_c = AB \cdot BB_1 = 2R \cdot BB_1\).
Согласно условию, отношение площади основания к площади сечения равно \(\frac{\sqrt{3}\pi}{4}\). Запишем это соотношение, подставив формулы для \(S\) и \(S_c\):
\(\frac{S}{S_c} = \frac{\pi R^2}{2R \cdot BB_1} = \frac{\sqrt{3}\pi}{4}\)
Упростим левую часть равенства:
\(\frac{\pi R}{2 \cdot BB_1} = \frac{\sqrt{3}\pi}{4}\)
Разделим обе части на \(\pi\):
\(\frac{R}{2 \cdot BB_1} = \frac{\sqrt{3}}{4}\)
Умножим обе части на 2:
\(\frac{R}{BB_1} = \frac{2\sqrt{3}}{4} = \frac{\sqrt{3}}{2}\)
Таким образом, мы получили соотношение между радиусом основания и высотой цилиндра.
Далее, рассмотрим прямоугольный треугольник \(ABB_1\). Угол \(\angle B_1 AB\) — это угол между диагональю сечения \(AB_1\) и диаметром основания \(AB\). Котангенс этого угла определяется как отношение прилежащего катета к противолежащему катету:
\(\text{ctg}\angle B_1 AB = \frac{AB}{BB_1}\)
Мы знаем, что \(AB = 2R\). Из предыдущего шага мы выразили \(\frac{R}{BB_1} = \frac{\sqrt{3}}{2}\), что эквивалентно \(BB_1 = \frac{2R}{\sqrt{3}}\). Подставим эти значения в формулу котангенса:
\(\text{ctg}\angle B_1 AB = \frac{2R}{\frac{2R}{\sqrt{3}}} = 2R \cdot \frac{\sqrt{3}}{2R} = \sqrt{3}\)
Нам известно, что котангенс угла в \(30^\circ\) равен \(\sqrt{3}\). Следовательно, \(\angle B_1 AB = 30^\circ\).
Теперь рассмотрим треугольник \(OAB\), где \(O\) — центр основания, а \(A\) и \(B\) — точки на окружности основания, образующие диаметр. Треугольник \(OAB\) является равнобедренным, так как \(OA\) и \(OB\) являются радиусами основания, поэтому \(OA = OB = R\). В равнобедренном треугольнике углы при основании равны, то есть \(\angle OAB = \angle OBA\).
Следуя примеру решения, принимаем, что \(\angle OAB = 30^\circ\). Тогда \(\angle OBA = 30^\circ\). Сумма углов в любом треугольнике равна \(180^\circ\). Следовательно, угол при вершине \(O\) в треугольнике \(OAB\) равен:
\(\angle BOA = 180^\circ — (\angle OAB + \angle OBA)\)
\(\angle BOA = 180^\circ — (30^\circ + 30^\circ)\)
\(\angle BOA = 180^\circ — 60^\circ\)
\(\angle BOA = 120^\circ\)
Таким образом, угол \(\angle BOA\) равен \(120^\circ\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.