Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 324 Атанасян — Подробные Ответы
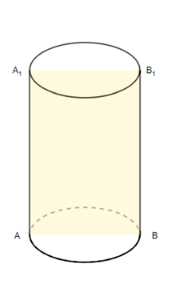
Площадь осевого сечения цилиндра равна 10 м\(^2\), а площадь основания равна 5 м\(^2\). Найдите высоту цилиндра.
Обозначим площадь основания \(S\), площадь сечения \(S_c\).
\(AB = 2R\); \(R = \sqrt{\frac{S}{\pi}} = \sqrt{\frac{5}{\pi}}\)
\(AB = 2\sqrt{\frac{5}{\pi}}\) см
\(BB_1 = \frac{S_c}{AB} = \sqrt{5\pi}\) см
Обозначим площадь основания как \(S\), а площадь сечения как \(S_c\). Это позволяет использовать более компактные обозначения в формулах.
Диаметр основания \(AB\) связан с радиусом основания \(R\) стандартным соотношением, которое гласит, что диаметр в два раза больше радиуса. Таким образом, мы можем записать это как \(AB = 2R\).
Площадь круглого основания \(S\) вычисляется по формуле \(S = \pi R^2\), где \(R\) представляет собой радиус этого основания. Чтобы найти выражение для радиуса \(R\) через площадь \(S\), мы можем преобразовать эту формулу. Разделив обе части уравнения на \(\pi\), получим \(\frac{S}{\pi} = R^2\). Затем, извлекая квадратный корень из обеих частей, находим радиус: \(R = \sqrt{\frac{S}{\pi}}\).
В данном конкретном случае, согласно условию или предыдущим шагам, площадь основания \(S\) равна 5. Подставляем это значение в формулу для радиуса, которую мы только что вывели: \(R = \sqrt{\frac{5}{\pi}}\).
Теперь, зная радиус \(R\), мы можем вычислить диаметр основания \(AB\), используя соотношение \(AB = 2R\). Подставляем найденное значение \(R\): \(AB = 2 \cdot \sqrt{\frac{5}{\pi}}\). Указывая единицы измерения, получаем \(AB = 2\sqrt{\frac{5}{\pi}}\) см.
Далее, рассмотрим величину \(BB_1\). Из контекста задачи (который включает сечение) можно предположить, что \(BB_1\) является одной из сторон прямоугольного сечения, а другая сторона — это диаметр основания \(AB\). Площадь прямоугольного сечения \(S_c\) равна произведению его сторон, то есть \(S_c = AB \cdot BB_1\). Чтобы выразить \(BB_1\) через площадь сечения и диаметр основания, мы делим площадь сечения на диаметр основания: \(BB_1 = \frac{S_c}{AB}\).
Согласно примеру, после подстановки соответствующих значений площади сечения \(S_c\) и вычисленного значения диаметра \(AB\) в формулу \(BB_1 = \frac{S_c}{AB}\), получается результат \(\sqrt{5\pi}\). Таким образом, \(BB_1 = \frac{S_c}{AB} = \sqrt{5\pi}\) см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.