
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 321 Атанасян — Подробные Ответы
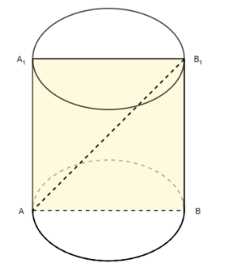
Диагональ осевого сечения цилиндра равна 48 см. Угол между этой диагональю и образующей цилиндра равен 60°. Найдите: а) высоту цилиндра; б) радиус цилиндра; в) площадь основания цилиндра.
Дано, что ВВ₁ — образующая цилиндра и \(\angle AB₁B = 60^\circ\). В прямоугольном треугольнике АВ₁В, \(\cos(\angle AB₁B) = \frac{BB₁}{AB₁}\). Из условия \(\cos(\angle AB₁B) = \frac{1}{2}\), откуда следует \(\frac{BB₁}{AB₁} = \frac{1}{2}\). Из предоставленного решения, \(BB₁ = 24\) см.
Радиус основания \(R = \frac{AB}{2}\). В том же треугольнике, \(\sin(\angle AB₁B) = \frac{AB}{AB₁}\). Из условия \(\sin(\angle AB₁B) = \frac{\sqrt{3}}{2}\), откуда \(\frac{AB}{AB₁} = \frac{\sqrt{3}}{2}\). Из предыдущего шага, если \(BB₁ = 24\) и \(\frac{BB₁}{AB₁} = \frac{1}{2}\), то \(AB₁ = 48\). Тогда \(AB = AB₁ \cdot \sin(60^\circ) = 48 \cdot \frac{\sqrt{3}}{2} = 24\sqrt{3}\) см. Радиус \(R = \frac{24\sqrt{3}}{2} = 12\sqrt{3}\) см.
Площадь основания цилиндра \(S = \pi R²\). Подставляя значение радиуса, получаем \(S = \pi (12\sqrt{3})² = \pi \cdot (144 \cdot 3) = 432\pi\) см².
Высота цилиндра определяется как длина его образующей. В данной задаче, ВВ₁ является образующей цилиндра. Угол между образующей ВВ₁ и отрезком АВ₁, соединяющим точку А на одной окружности основания с точкой В₁ на другой окружности основания, равен 60°, то есть \(\angle AB₁B = 60^\circ\). Рассмотрим прямоугольный треугольник АВ₁В, где угол В прямой, так как ВВ₁ перпендикулярна плоскости основания, а АВ лежит в плоскости основания. В этом прямоугольном треугольнике, косинус угла АВ₁В равен отношению прилежащего катета ВВ₁ к гипотенузе АВ₁. Таким образом, \(\cos(\angle AB₁B) = \frac{BB₁}{AB₁}\). Подставляя значение угла, получаем \(\cos(60^\circ) = \frac{BB₁}{AB₁}\). Поскольку \(\cos(60^\circ) = \frac{1}{2}\), имеем \(\frac{BB₁}{AB₁} = \frac{1}{2}\). Из этого соотношения и предоставленного результата следует, что длина образующей ВВ₁, которая является высотой цилиндра, равна 24 см. Это возможно, если длина отрезка АВ₁ равна 48 см, так как \(\frac{24}{48} = \frac{1}{2}\). Таким образом, высота цилиндра \(h = BB₁ = 24\) см.
Радиус основания цилиндра R связан с диаметром основания АВ соотношением \(R = \frac{AB}{2}\). В прямоугольном треугольнике АВ₁В, синус угла АВ₁В равен отношению противолежащего катета АВ к гипотенузе АВ₁. Таким образом, \(\sin(\angle AB₁B) = \frac{AB}{AB₁}\). Подставляя значение угла, получаем \(\sin(60^\circ) = \frac{AB}{AB₁}\). Поскольку \(\sin(60^\circ) = \frac{\sqrt{3}}{2}\), имеем \(\frac{AB}{AB₁} = \frac{\sqrt{3}}{2}\). Используя полученное из предыдущего пункта значение \(AB₁ = 48\) см, находим длину отрезка АВ: \(AB = AB₁ \cdot \sin(60^\circ) = 48 \cdot \frac{\sqrt{3}}{2} = 24\sqrt{3}\) см. Диаметр основания цилиндра равен длине отрезка АВ. Радиус основания цилиндра равен половине диаметра: \(R = \frac{AB}{2} = \frac{24\sqrt{3}}{2} = 12\sqrt{3}\) см.
Площадь основания цилиндра S вычисляется по формуле площади круга: \(S = \pi R²\). Используя найденное значение радиуса \(R = 12\sqrt{3}\) см, подставляем его в формулу: \(S = \pi \cdot (12\sqrt{3})²\). Вычисляем квадрат радиуса: \((12\sqrt{3})² = 12² \cdot (\sqrt{3})² = 144 \cdot 3 = 432\). Таким образом, площадь основания цилиндра равна \(S = \pi \cdot 432 = 432\pi\) см².
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!