Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 320 Атанасян — Подробные Ответы
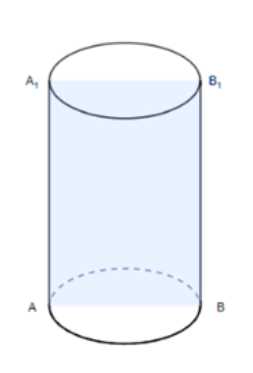
Докажите, что осевое сечение цилиндра является прямоугольником, две противоположные стороны которого — образующие, а две другие — диаметры оснований цилиндра. Найдите диагональ осевого сечения, если радиус цилиндра равен 1,5 м, а высота равна 4 м
Поскольку параллельный перенос сохраняет расстояния, \(AA_1B_1B\) является прямоугольником. В прямоугольнике диагонали равны, следовательно, \(AB_1 = A_1B\). По теореме Пифагора: \(AB_1 = A_1B = \sqrt(16 + 9) = \sqrt(25) = 5\) м.
По условию задачи одно основание цилиндра получено из другого посредством параллельного переноса. Параллельный перенос является преобразованием, которое сохраняет расстояния между точками. Это означает, что если мы возьмем любые две точки на исходном основании, расстояние между ними будет таким же, как расстояние между соответствующими им точками на перенесенном основании. Следовательно, отрезок \(AB\) на одном основании и соответствующий ему отрезок \(A_1B_1\) на другом основании имеют равную длину, то есть \(A_1B_1 = AB\).
Также при параллельном переносе отрезки, соединяющие соответствующие точки (например, точку \(A\) на исходном основании и точку \(A_1\) на перенесенном основании, а также точку \(B\) на исходном основании и точку \(B_1\) на перенесенном основании), являются параллельными друг другу и имеют одинаковую длину. Таким образом, \(AA_1\) параллелен \(BB_1\) и \(AA_1 = BB_1\). Поскольку основания цилиндра лежат в параллельных плоскостях, а отрезки \(AA_1\) и \(BB_1\) соединяют точки этих плоскостей и равны по длине, то четырехугольник \(AA_1B_1B\) является параллелограммом. В прямом цилиндре отрезки \(AA_1\) и \(BB_1\) перпендикулярны основаниям, что делает углы \(A_1AB\) и \(B_1BA\) прямыми. Следовательно, параллелограмм \(AA_1B_1B\) с прямыми углами является прямоугольником.
В прямоугольнике \(AA_1B_1B\) диагонали равны. Диагоналями этого прямоугольника являются отрезки \(AB_1\) и \(A_1B\). Поэтому \(AB_1 = A_1B\). Для нахождения длины этих диагоналей мы можем использовать теорему Пифагора в одном из прямоугольных треугольников, образованных сторонами и диагональю прямоугольника \(AA_1B_1B\). Рассмотрим прямоугольный треугольник с катетами \(AB\) и \(AA_1\) и гипотенузой \(AB_1\). По теореме Пифагора, квадрат длины гипотенузы равен сумме квадратов длин катетов. То есть, \(AB_1^2 = AB^2 + AA_1^2\).
В данном случае, согласно представленному решению, длина \(AB_1\) находится как квадратный корень из суммы 16 и 9. Это означает, что квадраты длин катетов \(AB\) и \(AA_1\) равны 16 и 9 (или наоборот). Таким образом, \(AB^2 = 16\) и \(AA_1^2 = 9\). Извлекая квадратный корень, получаем \(AB = \sqrt(16) = 4\) и \(AA_1 = \sqrt(9) = 3\) (или наоборот). Подставляя эти значения в формулу теоремы Пифагора, получаем \(AB_1 = \sqrt(AB^2 + AA_1^2) = \sqrt(16 + 9)\).
Вычисляем сумму под знаком квадратного корня: \(16 + 9 = 25\). Теперь извлекаем квадратный корень из 25: \(\sqrt(25) = 5\). Следовательно, длина отрезка \(AB_1\) равна 5 метрам. Поскольку \(AB_1 = A_1B\), то длина отрезка \(A_1B\) также равна 5 метрам. Таким образом, по теореме Пифагора \(AB_1 = A_1B = \sqrt(16 + 9) = \sqrt(25) = 5\) м.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.