
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 319 Атанасян — Подробные Ответы
Сколько плоскостей симметрии, проходящих через данную вершину, имеет правильный тетраэдр?
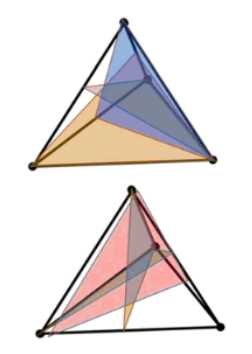
Плоскость симметрии правильного тетраэдра проходит через ребро и середину противоположного ребра.
Поскольку через каждую вершину проходят три ребра, то через одну вершину правильного тетраэдра можно провести три плоскости симметрии.
Начнем с того, что у каждого правильного тетраэдра имеется шесть плоскостей симметрии, как это было показано в задаче 278.
Плоскость симметрии правильного тетраэдра определяется тем, что она проходит через одно из ребер тетраэдра и середину ребра, противоположного выбранному. Рассмотрим теперь одну из вершин правильного тетраэдра. Через каждую вершину правильного тетраэдра проходят три ребра. Для того чтобы плоскость симметрии проходила через выбранную вершину, эта плоскость должна содержать одно из ребер, выходящих из данной вершины. Каждому ребру, выходящему из вершины, соответствует единственное противоположное ребро. Плоскость, проходящая через ребро, выходящее из рассматриваемой вершины, и середину противоположного ему ребра, является плоскостью симметрии и при этом содержит выбранную вершину. Поскольку из каждой вершины правильного тетраэдра выходят три ребра, и каждое такое ребро в сочетании с серединой противоположного ребра определяет уникальную плоскость симметрии, проходящую через данную вершину, то через одну вершину правильного тетраэдра можно провести три плоскости симметрии. Таким образом, количество плоскостей симметрии, которые можно провести через одну вершину правильного тетраэдра, равно трем.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!