ГДЗ по Геометрии 10 класс Номер 318 Атанасян — Подробные Ответы

Докажите, что сумма двугранного угла правильного тетраэдра и двугранного угла правильного октаэдра равна \(180^\circ\).

Дано правильный тетраэдр и правильный октаэдр. Требуется доказать, что сумма их двугранных углов равна 180°.

Для правильного октаэдра, используя теорему косинусов в соответствующем сечении, где \(AB = (\sqrt{2} \cdot a)\) и \(BC = AC = h_{\text{грани}} = (\frac{\sqrt{3} \cdot a}{2})\), косинус двугранного угла \(\angle ACB\) находится как \(\cos(\angle ACB) = (\frac{BC^2 + AC^2 — AB^2}{2 \cdot BC \cdot AC})\). Подстановка значений дает \(\cos(\angle ACB) = (\frac{(\frac{3 \cdot a^2}{4}) + (\frac{3 \cdot a^2}{4}) — (2 \cdot a^2)}{2 \cdot (\frac{\sqrt{3} \cdot a}{2}) \cdot (\frac{\sqrt{3} \cdot a}{2})}) = (-\frac{1}{3})\).

Для правильного тетраэдра, косинус двугранного угла \(\angle A_1C_1B_1\) равен отношению \(A_1C_1\) к \(C_1B_1\). Известно, что \(A_1C_1 = (\frac{h_{\text{грани}}}{3})\) и \(C_1B_1 = h_{\text{грани}}\). Следовательно, \(\cos(\angle A_1C_1B_1) = (\frac{(\frac{h_{\text{грани}}}{3})}{h_{\text{грани}}}) = (\frac{1}{3})\).

Поскольку косинусы двугранных углов равны \(-\frac{1}{3}\) и \(\frac{1}{3}\), они противоположны, что означает, что сумма углов равна 180°. Что и требовалось доказать.

Дано правильный тетраэдр и правильный октаэдр. Необходимо доказать, что сумма двугранного угла правильного тетраэдра и двугранного угла правильного октаэдра равна 180°.

Для решения задачи воспользуемся известными соотношениями из геометрии правильных многогранников.

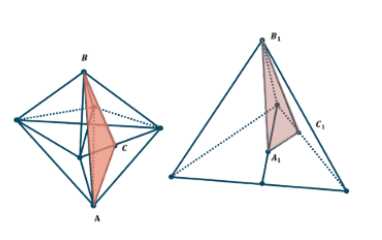
Рассмотрим построение, связанное с двугранным углом правильного октаэдра. В этом построении отрезок \(AB\) представляет собой удвоенную высоту правильной пирамиды, составляющей половину октаэдра. Длина этого отрезка равна \((\sqrt{2} \cdot a)\), где \(a\) — длина ребра октаэдра.

Отрезки \(BC\) и \(AC\) являются апофемами граней октаэдра. Апофема правильного треугольника со стороной \(a\) равна \((\frac{\sqrt{3} \cdot a}{2})\). Таким образом, \(BC = AC = h_{\text{грани}} = (\frac{\sqrt{3} \cdot a}{2})\).

Рассмотрим построение, связанное с двугранным углом правильного тетраэдра. Отрезок \(C_1B_1\) также является апофемой грани тетраэдра, то есть \(C_1B_1 = h_{\text{грани}}\). Отрезок \(A_1C_1\) представляет собой треть высоты основания тетраэдра, которая также равна апофеме грани. Это связано с тем, что основание высоты тетраэдра проецируется в центр правильного треугольника основания, а расстояние от центра до середины стороны составляет одну треть медианы (высоты) этого треугольника. Следовательно, \(A_1C_1 = (\frac{h_{\text{грани}}}{3})\).

Теперь применим теорему косинусов к треугольнику \(ABC\), где угол \(\angle ACB\) является двугранным углом правильного октаэдра. По теореме косинусов имеем: \(AB^2 = BC^2 + AC^2 — 2 \cdot BC \cdot AC \cdot \cos(\angle ACB)\).

Выразим косинус угла \(\angle ACB\): \(\cos(\angle ACB) = (\frac{BC^2 + AC^2 — AB^2}{2 \cdot BC \cdot AC})\).

Подставим известные значения длин отрезков:
\(BC^2 = (h_{\text{грани}})^2 = (\frac{\sqrt{3} \cdot a}{2})^2 = (\frac{3 \cdot a^2}{4})\)
\(AC^2 = (h_{\text{грани}})^2 = (\frac{\sqrt{3} \cdot a}{2})^2 = (\frac{3 \cdot a^2}{4})\)
\(AB^2 = (\sqrt{2} \cdot a)^2 = (2 \cdot a^2)\)

Теперь подставим эти значения в формулу для косинуса \(\angle ACB\):
\(\cos(\angle ACB) = (\frac{(\frac{3 \cdot a^2}{4}) + (\frac{3 \cdot a^2}{4}) — (2 \cdot a^2)}{2 \cdot (\frac{\sqrt{3} \cdot a}{2}) \cdot (\frac{\sqrt{3} \cdot a}{2})})\)
\(\cos(\angle ACB) = (\frac{(\frac{6 \cdot a^2}{4}) — (2 \cdot a^2)}{2 \cdot (\frac{3 \cdot a^2}{4})})\)
\(\cos(\angle ACB) = (\frac{(\frac{3 \cdot a^2}{2}) — (\frac{4 \cdot a^2}{2})}{(\frac{3 \cdot a^2}{2})})\)
\(\cos(\angle ACB) = (\frac{(-\frac{1 \cdot a^2}{2})}{(\frac{3 \cdot a^2}{2})})\)
\(\cos(\angle ACB) = (-\frac{1}{3})\).

Теперь рассмотрим двугранный угол правильного тетраэдра. В соответствующем построении, косинус двугранного угла \(\angle A_1C_1B_1\) выражается через отношение отрезков \(A_1C_1\) и \(C_1B_1\). Как было установлено, \(A_1C_1 = (\frac{h_{\text{грани}}}{3})\) и \(C_1B_1 = h_{\text{грани}}\).
Следовательно, \(\cos(\angle A_1C_1B_1) = (\frac{A_1C_1}{C_1B_1}) = (\frac{(\frac{h_{\text{грани}}}{3})}{h_{\text{грани}}}) = (\frac{1}{3})\).

Таким образом, косинус двугранного угла правильного октаэдра равен \(-\frac{1}{3}\), а косинус двугранного угла правильного тетраэдра равен \(\frac{1}{3}\). Поскольку косинусы этих двух углов являются противоположными числами, это означает, что сами углы в сумме дают 180°.

Что и требовалось доказать.