Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 317 Атанасян — Подробные Ответы
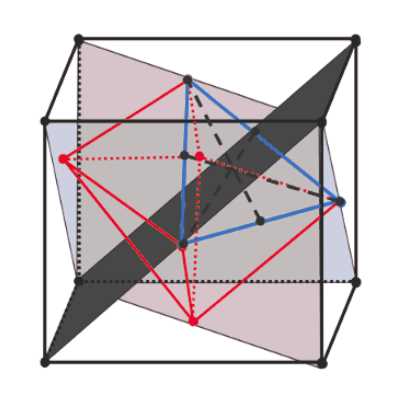
Докажите, что центры граней куба являются вершинами правильного октаэдра.
Решение основано на симметрии.
Центры граней куба образуют вершины искомого многогранника. Этот многогранник наследует плоскости симметрии исходного куба, которых девять. Каждая грань полученного многогранника является треугольником, образованным центрами трех смежных граней куба. Эти треугольники являются правильными (равносторонними), что можно показать, вычислив длины их сторон. Если сторона куба равна \(s\), то расстояние между центрами смежных граней равно \(s/\sqrt{2}\), и все стороны треугольных граней имеют эту длину. Поперечное сечение многогранника, проходящее через центры четырех несмежных граней, представляет собой квадрат. Многогранник с шестью вершинами, восьмью равносторонними треугольными гранями и квадратным поперечным сечением является правильным октаэдром. Следовательно, искомый многогранник — правильный октаэдр.
Рассмотрим куб. У куба шесть граней. Найдем центры этих шести граней. Эти шесть точек будут вершинами многогранника, который нас интересует.
Теперь подумаем о связях между этими точками. Рисунок показывает, что вершины вписанной красной фигуры, которая названа октаэдром, расположены в центрах граней куба. Ребра этой вписанной фигуры соединяют центры смежных граней куба.
Давайте рассмотрим симметрию куба. Куб обладает высокой степенью симметрии. Решение упоминает, что правильный октаэдр имеет 9 плоскостей симметрии. Многогранник, образованный центрами граней куба, наследует симметрию куба. Куб также имеет 9 плоскостей симметрии. Эти плоскости симметрии куба являются также плоскостями симметрии фигуры, образованной его центрами граней. Это сохранение симметрии является ключевым моментом в рассуждении решения.
Решение утверждает, что каждая грань полученного многогранника — треугольник. Давайте посмотрим, как образуются эти треугольники. Вершинами нашего нового многогранника являются центры граней куба. Рассмотрим вершину куба. Три грани куба сходятся в этой вершине. Центры этих трех граней образуют треугольник. Например, если мы рассмотрим верхнюю-переднюю-правую вершину куба, центры верхней грани, передней грани и правой грани образуют треугольник. У куба 8 вершин, и каждая соответствует одному такому треугольнику, образованному центрами трех смежных граней. Таким образом, полученный многогранник имеет 8 треугольных граней. Это совпадает с числом граней у октаэдра.
Решение также утверждает, что каждый треугольник имеет три плоскости симметрии, проходящие через середину стороны и через противоположную вершину. Это свойство характерно для правильных (равносторонних) треугольников. Давайте проверим, являются ли треугольники равносторонними.
Пусть длина стороны куба равна \(s\). Мы можем поместить центр куба в начало координат \((0, 0, 0)\). Тогда центры граней будут иметь координаты, например, \((\pm s/2, 0, 0)\), \((0, \pm s/2, 0)\) и \((0, 0, \pm s/2)\).
Рассмотрим центры верхней грани \((0, 0, s/2)\), передней грани \((0, s/2, 0)\) и правой грани \((s/2, 0, 0)\). Эти три точки образуют одну из треугольных граней вписанного многогранника. Вычислим длины сторон этого треугольника.
Расстояние между \((0, 0, s/2)\) и \((0, s/2, 0)\) равно \(\sqrt{(0-0)^2 + (s/2-0)^2 + (0-s/2)^2} = \sqrt{(s/2)^2 + (-s/2)^2} = \)
\(=\sqrt{s^2/4 + s^2/4} = \sqrt{s^2/2} = s/\sqrt{2}\).
Расстояние между \((0, s/2, 0)\) и \((s/2, 0, 0)\) равно \(\sqrt{(s/2-0)^2 + (0-s/2)^2 + (0-0)^2} = \sqrt{(s/2)^2 + (-s/2)^2} = \)
\(=\sqrt{s^2/4 + s^2/4} = \sqrt{s^2/2} = s/\sqrt{2}\).
Расстояние между \((s/2, 0, 0)\) и \((0, 0, s/2)\) равно \(\sqrt{(0-s/2)^2 + (0-0)^2 + (s/2-0)^2} = \sqrt{(-s/2)^2 + (s/2)^2} = \)
\(=\sqrt{s^2/4 + s^2/4} = \sqrt{s^2/2} = s/\sqrt{2}\).
Поскольку все три стороны треугольника имеют одинаковую длину \(s/\sqrt{2}\), треугольник является равносторонним.
Решение утверждает, что полученный треугольник правильный, что в данном контексте означает равносторонний. Это подтверждает наш расчет.
Решение также упоминает, что в поперечном сечении очевидно квадрат. Рассмотрим плоскость, которая разрезает куб и проходит через центры четырех несмежных граней, например, центры верхней, нижней, передней и задней граней. Эти четыре центра лежат в одной плоскости и образуют квадрат. Этот квадрат является поперечным сечением вписанного многогранника. Это наблюдение дополнительно подтверждает вывод о том, что вписанная фигура является октаэдром, поскольку квадратное сечение, проходящее через центр, характерно для октаэдра.
Исходя из того, что многогранник, образованный центрами граней куба, имеет 6 вершин, 12 ребер равной длины и 8 равносторонних треугольных граней, он соответствует определению правильного октаэдра. Аргумент симметрии также подтверждает этот вывод. Решение заключает, что искомый многогранник — правильный октаэдр.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.