
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 316 Атанасян — Подробные Ответы
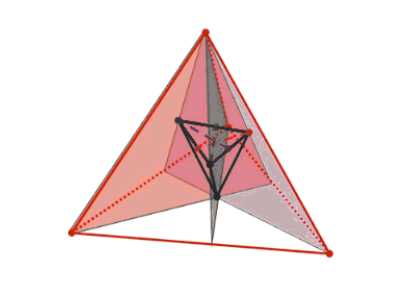
Докажите, что центры граней правильного тетраэдра являются вершинами другого правильного тетраэдра.
Решение основано на использовании симметрии. Правильный тетраэдр имеет шесть плоскостей симметрии.
Многогранник, построенный на центрах граней исходного тетраэдра, сохраняет эти плоскости симметрии. Полученный многогранник имеет четыре грани, каждая из которых является треугольником. Каждый такой треугольник имеет три плоскости симметрии, проходящие через середину стороны и противоположную вершину, что указывает на то, что эти треугольники являются правильными. Следовательно, искомый многогранник с четырьмя правильными треугольными гранями является правильным тетраэдром.
Итак, дан правильный тетраэдр. Известно, что каждый правильный тетраэдр обладает шестью плоскостями симметрии.
Рассматривается многогранник, построенный таким образом, что его вершины совпадают с центрами граней исходного правильного тетраэдра. Отмечается, что многогранник, построенный на симметричных точках исходной фигуры, сохраняет ее плоскости симметрии, следовательно, у этого нового многогранника также имеется шесть плоскостей симметрии. Указывается, что полученный многогранник имеет четыре грани. Далее описывается форма каждой грани этого полученного многогранника, а именно, что каждая его грань является треугольником. Уточняется, что каждый из этих треугольников обладает тремя плоскостями симметрии. Эти плоскости симметрии проходят через середину каждой стороны треугольника и соответствующую противоположную вершину, что проиллюстрировано на рисунке. Из того факта, что каждый треугольник имеет три такие плоскости симметрии, следует, что этот треугольник является правильным. На основании того, что искомый многогранник имеет четыре грани, и каждая из этих граней представляет собой правильный треугольник, делается вывод, что сам искомый многогранник является правильным тетраэдром.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!