
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 314 Атанасян — Подробные Ответы
В правильной четырёхугольной усечённой пирамиде высота равна 63 см, апофема — 65 см, а стороны оснований относятся как \(7 : 3\). Найдите стороны оснований пирамиды.
Обозначим сторону меньшего основания \(A_1B_1\) как \(3x\), тогда сторона большего основания \(AB\) равна \(7x\).
Из построения следует, что \(KH = \frac{1}{2}(AB — A_1B_1) = \frac{1}{2}(7x — 3x) = 2x\). В прямоугольном треугольнике \(KH_1H\) по теореме Пифагора \(KH^2 + H_1K^2 = HH_1^2\), где \(H_1K = OO_1 = 63\). Получаем уравнение \((2x)^2 + (63)^2 = (65)^2\). Решая его, находим \(4x^2 + 3969 = 4225\), \(4x^2 = 256\), \(x^2 = 64\), откуда \(x = 8\). Тогда \(A_1B_1 = 3 \cdot 8 = 24\) см, а \(AB = 7 \cdot 8 = 56\) см. Ответ: \(A_1B_1 = 24\) см, \(AB = 56\) см.
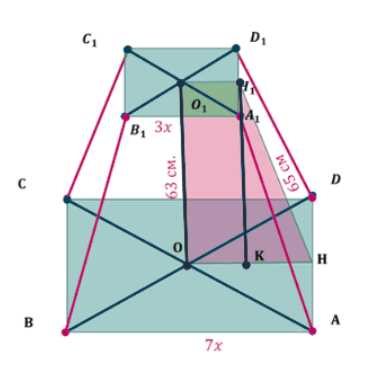
Дано, что \(ABCDA_1B_1C_1D_1\) — это усеченная пирамида. Известно, что \(K\) — основание высоты, опущенной из верхней точки апофемы \(H_1H\). Длина отрезка \(HH_1\) равна 65 см, а длина отрезка \(OO_1\) равна 63 см. Плоскость верхнего основания \(A_1B_1C_1D_1\) параллельна плоскости нижнего основания \(ABCD\), и точка \(O_1\) принадлежит плоскости \(A_1B_1C_1D_1\). Отношение длины стороны \(A_1B_1\) к длине стороны \(AB\) равно \(\frac{3}{7}\). Требуется найти длины сторон \(AB\) и \(A_1B_1\).
Для решения задачи обозначим сторону меньшего основания усеченной пирамиды \(A_1B_1\) как \(3x\). Из данного отношения сторон \(\frac{A_1B_1}{AB} = \frac{3}{7}\) следует, что если \(A_1B_1 = 3x\), то \(AB\) будет равно \(7x\).
Рассмотрим построение, при котором образуется прямоугольный треугольник \(KH_1H\). В этом треугольнике отрезок \(KH\) представляет собой разность между половинами диагоналей оснований, или, более точно, разность между отрезками \(HO\) и \(OK\). Отрезок \(HO\) является половиной диагонали нижнего основания, а отрезок \(OK\) связан с половиной диагонали верхнего основания. Из подобия треугольников можно показать, что \(KH = HO — OK = \frac{1}{2}(AB — A_1B_1)\). Подставляя выражения для \(AB\) и \(A_1B_1\) через \(x\), получаем \(KH = \frac{1}{2}(7x — 3x) = \frac{1}{2}(4x) = 2x\).
Теперь применим теорему Пифагора к прямоугольному треугольнику \(KH_1H\). В этом треугольнике гипотенузой является отрезок \(HH_1\), а катетами — отрезки \(KH\) и \(H_1K\). Длина отрезка \(H_1K\) равна высоте усеченной пирамиды \(OO_1\), то есть \(H_1K = OO_1 = 63\) см. По теореме Пифагора имеем \(KH^2 + H_1K^2 = HH_1^2\). Подставляя известные значения и выражение для \(KH\), получаем \((2x)^2 + (63)^2 = (65)^2\).
Вычисляем квадраты: \(4x^2 + 3969 = 4225\). Вычитаем 3969 из обеих частей уравнения: \(4x^2 = 4225 — 3969\), что дает \(4x^2 = 256\). Делим обе части на 4: \(x^2 = \frac{256}{4}\), откуда \(x^2 = 64\). Извлекая квадратный корень, находим значение \(x\): \(x = \sqrt{64} = 8\) см.
Теперь, используя найденное значение \(x\), вычислим длины сторон оснований. Сторона меньшего основания \(A_1B_1\) равна \(3x\), следовательно, \(A_1B_1 = 3 \cdot 8 = 24\) см. Сторона большего основания \(AB\) равна \(7x\), следовательно, \(AB = 7 \cdot 8 = 56\) см.
Таким образом, длина стороны \(A_1B_1\) составляет 24 см, а длина стороны \(AB\) составляет 56 см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!