Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 313 Атанасян — Подробные Ответы
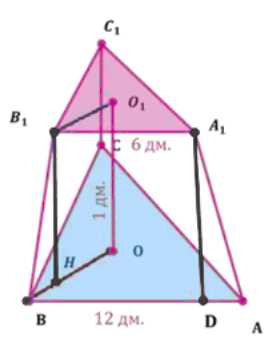
Стороны оснований правильной треугольной усечённой пирамиды равны 12 дм и 6 дм, а её высота 1 дм. Найдите площадь боковой поверхности пирамиды.
Площадь боковой поверхности правильной усеченной пирамиды равна утроенной площади боковой грани, которая является равнобедренной трапецией \(ABB_1A_1\). \(S_{\text{боковой}} = 3 \cdot S_{ABB_1A_1}\). Площадь трапеции \(ABB_1A_1\) равна \(\frac{(AB + A_1B_1)}{2} \cdot A_1D\), где \(A_1D\) — апофема (высота трапеции).
Радиусы описанных окружностей нижнего и верхнего оснований равны \(R_{ABC} = \frac{AB}{\sqrt{3}} = \frac{12}{\sqrt{3}}\) и \(R_{A_1B_1C_1} = \frac{A_1B_1}{\sqrt{3}} = \frac{6}{\sqrt{3}}\). Разность этих радиусов равна \(HB = R_{ABC} — R_{A_1B_1C_1} = \frac{12}{\sqrt{3}} — \frac{6}{\sqrt{3}} = \frac{6}{\sqrt{3}} = 2\sqrt{3}\) дм.
Боковое ребро \(B_1B\) найдем из прямоугольного треугольника с катетами \(O_1O\) и \(HB\). По теореме Пифагора, \(B_1B = \sqrt{(O_1O)^2 + (HB)^2} = \sqrt{1^2 + (2\sqrt{3})^2} = \sqrt{1 + 12} = \sqrt{13}\) дм.
В равнобедренной трапеции \(ABB_1A_1\), отрезок \(AD\), образованный при опускании высоты \(A_1D\), равен половине разности оснований: \(AD = \frac{(AB — A_1B_1)}{2} = \frac{(12 — 6)}{2} = 3\) дм.
Апофему \(A_1D\) найдем из прямоугольного треугольника \(AA_1D\) (или \(BB_1H\)), где \(AA_1 = B_1B = \sqrt{13}\) — гипотенуза, а \(AD = 3\) — катет. По теореме Пифагора, \(A_1D = \sqrt{(AA_1)^2 — (AD)^2} = \sqrt{(\sqrt{13})^2 — 3^2} = \sqrt{13 — 9} = \sqrt{4} = 2\) дм.
Площадь боковой грани \(ABB_1A_1\) равна \(S_{ABB_1A_1} = \frac{(AB + A_1B_1)}{2} \cdot A_1D = \frac{(12 + 6)}{2} \cdot 2 = \frac{18}{2} \cdot 2 = 9 \cdot 2 = 18\) дм².
Площадь боковой поверхности пирамиды равна \(S_{\text{боковой}} = 3 \cdot S_{ABB_1A_1} = 3 \cdot 18 = 54\) дм².
Ответ: \(54\) дм².
Задача состоит в нахождении площади боковой поверхности усеченной правильной пирамиды \(ABCA_1B_1C_1\). Известно, что \(O\) — центр нижнего основания \(ABC\), \(O_1\) — центр верхнего основания \(A_1B_1C_1\), \(O_1O = 1\) дм, \(AB = 12\) дм, \(A_1B_1 = 6\) дм.
Так как пирамида является правильной, ее боковая поверхность состоит из трех равных трапеций. В данном случае это трапеции \(ABB_1A_1\), \(BCC_1B_1\) и \(CAA_1C_1\). Следовательно, площадь боковой поверхности \(S_{\text{боковой}}\) равна утроенной площади одной такой трапеции, например \(S_{ABB_1A_1}\). Это выражается формулой \(S_{\text{боковой}} = 3 \cdot S_{ABB_1A_1}\).
Трапеция \(ABB_1A_1\) является равнобедренной, так как боковые ребра правильной усеченной пирамиды равны. Высота этой трапеции, опущенная из вершины \(A_1\) на основание \(AB\), является апофемой боковой грани. Обозначим эту апофему как \(h\). Площадь трапеции \(ABB_1A_1\) вычисляется по формуле площади трапеции: полусумма оснований, умноженная на высоту. Основаниями являются стороны \(AB\) и \(A_1B_1\). Таким образом, \(S_{ABB_1A_1} = \frac{(AB + A_1B_1)}{2} \cdot h\). Подставляя известные значения сторон оснований, получаем \(S_{ABB_1A_1} = \frac{(12 + 6)}{2} \cdot h = \frac{18}{2} \cdot h = 9h\). В решении задачи апофема обозначена как \(A_1D\), поэтому \(S_{ABB_1A_1} = 9 \cdot A_1D\).
Для нахождения апофемы \(A_1D\) рассмотрим треугольник, образованный апофемой, высотой усеченной пирамиды и отрезком, соединяющим проекции вершин \(A_1\) и \(A\) на плоскость основания. В данном случае, из-за правильности пирамиды, этот отрезок лежит на прямой, проходящей через центры оснований \(O_1\) и \(O\). Однако, в решении используется другой подход, основанный на построении высоты трапеции \(ABB_1A_1\).
Рассмотрим равнобедренную трапецию \(ABB_1A_1\). Опустим перпендикуляр из вершины \(B_1\) на основание \(AB\), обозначив точку пересечения как \(H\). \(B_1H\) является высотой трапеции \(ABB_1A_1\). Для нахождения \(B_1H\) рассмотрим прямоугольный треугольник \(B_1HB\). В этом треугольнике \(B_1B\) является гипотенузой, а \(B_1H\) и \(HB\) — катетами.
Для нахождения длины отрезка \(HB\) рассмотрим нижнее и верхнее основания пирамиды. Они являются правильными треугольниками \(ABC\) и \(A_1B_1C_1\). Центры этих треугольников \(O\) и \(O_1\) являются также центрами описанных окружностей. Радиус описанной окружности правильного треугольника со стороной \(a\) равен \(R = \frac{a}{\sqrt{3}}\).
Радиус описанной окружности нижнего основания \(R_{ABC} = BO = \frac{AB}{\sqrt{3}} = \frac{12}{\sqrt{3}}\).
Радиус описанной окружности верхнего основания \(R_{A_1B_1C_1} = B_1O_1 = \frac{A_1B_1}{\sqrt{3}} = \frac{6}{\sqrt{3}}\).
Отрезок \(HB\) равен разности радиусов описанных окружностей: \(HB = BO — B_1O_1 = R_{ABC} — R_{A_1B_1C_1} = \frac{12}{\sqrt{3}} — \frac{6}{\sqrt{3}} = \frac{6}{\sqrt{3}} = 2\sqrt{3}\) дм.
Теперь найдем длину бокового ребра \(B_1B\). Рассмотрим прямоугольный треугольник, образованный боковым ребром \(B_1B\), высотой усеченной пирамиды \(O_1O\) и отрезком, соединяющим \(O\) и проекцию \(B_1\) на плоскость нижнего основания. Проекцией \(B_1\) является точка \(B’\) такая, что \(OB’\) лежит на прямой \(OB\) и \(OB’ = OB — B_1O_1\). В данном случае, из рисунка и свойств правильной пирамиды, можно рассмотреть прямоугольный треугольник с катетами \(O_1O\) и \(OB — O_1B_1\) и гипотенузой \(B_1B\). Однако, решение использует другой подход, находя \(B_1B\) из треугольника \(BB_1H\).
В прямоугольном треугольнике \(BB_1H\), катет \(B_1H\) является высотой трапеции \(ABB_1A_1\), которую мы ищем (апофема \(A_1D\)). Катет \(HB = 2\sqrt{3}\) дм. Для нахождения \(B_1H\) (или \(A_1D\)), нам нужно знать длину гипотенузы \(B_1B\).
Рассмотрим прямоугольный треугольник с катетами \(O_1O\) (высота усеченной пирамиды) и \(OB — O_1B_1\), и гипотенузой \(B_1B\). Катет \(O_1O = 1\) дм. Катет \(OB — O_1B_1 = R_{ABC} — R_{A_1B_1C_1} = 2\sqrt{3}\) дм. По теореме Пифагора, \(B_1B^2 = (O_1O)^2 + (OB — O_1B_1)^2 = 1^2 + (2\sqrt{3})^2 = 1 + 4 \cdot 3 = 1 + 12 = 13\). Следовательно, \(B_1B = \sqrt{13}\) дм.
Теперь вернемся к прямоугольному треугольнику \(BB_1H\). Гипотенуза \(B_1B = \sqrt{13}\) дм, катет \(HB = 2\sqrt{3}\) дм. По теореме Пифагора, \(B_1H^2 + HB^2 = B_1B^2\). \(B_1H^2 + (2\sqrt{3})^2 = (\sqrt{13})^2\). \(B_1H^2 + 12 = 13\). \(B_1H^2 = 13 — 12 = 1\). \(B_1H = \sqrt{1} = 1\) дм.
В решении задачи апофема обозначена как \(A_1D\). Рассмотрим прямоугольный треугольник \(AA_1D\), где \(A_1D\) — апофема (высота трапеции), \(AA_1\) — боковое ребро, и \(AD\) — половина разности длин оснований трапеции. Длина бокового ребра \(AA_1\) равна длине \(B_1B\), то есть \(AA_1 = \sqrt{13}\) дм. Длина отрезка \(AD\) в трапеции \(ABB_1A_1\), где \(A_1D\) — высота, равна \(\frac{(AB — A_1B_1)}{2} = \frac{(12 — 6)}{2} = \frac{6}{2} = 3\) дм.
Однако, в решении используется другое построение для нахождения апофемы \(A_1D\). Рассматривается прямоугольный треугольник с гипотенузой \(A_1A\) (боковое ребро) и катетами \(A_1D\) (апофема) и \(AD\). В решении указано, что \(AD = \frac{(AB — A_1B_1)}{2}\). Это соответствует построению высоты в равнобедренной трапеции. Таким образом, в прямоугольном треугольнике \(AA_1D\), по теореме Пифагора, \(A_1D^2 + AD^2 = AA_1^2\). \(A_1D^2 + (\frac{(AB — A_1B_1)}{2})^2 = (\sqrt{13})^2\). \(A_1D^2 + (\frac{(12 — 6)}{2})^2 = 13\). \(A_1D^2 + (\frac{6}{2})^2 = 13\). \(A_1D^2 + 3^2 = 13\). \(A_1D^2 + 9 = 13\). \(A_1D^2 = 13 — 9 = 4\). \(A_1D = \sqrt{4} = 2\) дм.
Таким образом, апофема боковой грани \(A_1D\) равна 2 дм.
Теперь мы можем вычислить площадь боковой поверхности. \(S_{\text{боковой}} = 3 \cdot S_{ABB_1A_1} = 3 \cdot (9 \cdot A_1D)\). Подставляя значение \(A_1D = 2\) дм, получаем \(S_{\text{боковой}} = 3 \cdot (9 \cdot 2) = 3 \cdot 18 = 54\) дм².
Ответ: Площадь боковой поверхности усеченной правильной пирамиды равна 54 дм².
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.