
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 312 Атанасян — Подробные Ответы
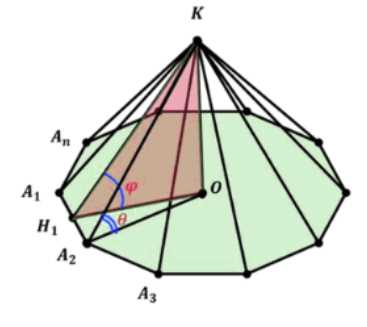
В правильной \(n\)-угольной пирамиде боковые грани составляют с плоскостью основания угол \(\varphi\). Найдите тангенс угла между плоскостью основания и боковым ребром.
Из прямоугольного треугольника \(KOA_1\) имеем \(\text{tg}(\theta) = \frac{KO}{OA_1}\).
Из треугольника \(OH_1A_1\) известно, что \(OH_1 = OA_1 \cdot \text{cos}(\frac{180^\circ}{n})\), откуда \(OA_1 = \frac{OH_1}{\text{cos}(\frac{180^\circ}{n})}\).
Подставляя это в выражение для \(\text{tg}(\theta)\), получаем \(\text{tg}(\theta) = \frac{KO}{\frac{OH_1}{\text{cos}(\frac{180^\circ}{n})}} = \frac{KO \cdot \text{cos}(\frac{180^\circ}{n})}{OH_1}\).
Перегруппировав, имеем \(\text{tg}(\theta) = \text{cos}(\frac{180^\circ}{n}) \cdot \frac{KO}{OH_1}\).
Из условия или рисунка видно, что \(\frac{KO}{OH_1} = \text{tg}(\phi)\).
Следовательно, \(\text{tg}(\theta) = \text{cos}(\frac{180^\circ}{n}) \cdot \text{tg}(\phi)\).
Из курса планиметрии известно, что \(OH_1\) является радиусом окружности, вписанной в правильный многоугольник, который лежит в основании пирамиды.
Рассмотрим прямоугольный треугольник \(KOA_1\). В этом треугольнике тангенс угла \(\theta\) определяется как отношение противолежащего катета \(KO\) к прилежащему катету \(OA_1\). Таким образом, мы имеем формулу \(\text{tg}(\theta) = \frac{KO}{OA_1}\).
Далее, рассмотрим треугольник \(OH_1A_1\), который также является прямоугольным. В этом треугольнике \(OH_1\) — это радиус вписанной окружности (апофема основания), а \(OA_1\) — это радиус описанной окружности вокруг основания. Угол \(\angle A_1OH_1\) равен половине центрального угла, стягиваемого стороной основания, то есть \(\frac{180^\circ}{n}\). В этом треугольнике косинус угла \(\frac{180^\circ}{n}\) равен отношению прилежащего катета \(OH_1\) к гипотенузе \(OA_1\). Следовательно, \(\text{cos}(\frac{180^\circ}{n}) = \frac{OH_1}{OA_1}\). Из этого соотношения мы можем выразить \(OA_1\) как \(OA_1 = \frac{OH_1}{\text{cos}(\frac{180^\circ}{n})}\).
Теперь подставим полученное выражение для \(OA_1\) в формулу для \(\text{tg}(\theta)\):
\(\text{tg}(\theta) = \frac{KO}{OA_1} = \frac{KO}{\frac{OH_1}{\text{cos}(\frac{180^\circ}{n})}}\).
Преобразуем это выражение, умножив числитель на знаменатель обратной дроби:
\(\text{tg}(\theta) = KO \cdot \frac{\text{cos}(\frac{180^\circ}{n})}{OH_1} = \frac{KO \cdot \text{cos}(\frac{180^\circ}{n})}{OH_1}\).
Перегруппируем члены в числителе:
\(\text{tg}(\theta) = \text{cos}(\frac{180^\circ}{n}) \cdot \frac{KO}{OH_1}\).
Теперь рассмотрим прямоугольный треугольник \(KOH_1\). В этом треугольнике отношение \(\frac{KO}{OH_1}\) представляет собой тангенс угла \(\angle KH_1O\). Согласно шагам решения, это отношение приравнивается к \(\text{tg}(\phi)\), где \(\phi\) — это угол, для которого \(\text{tg}(\phi) = \frac{KO}{OH_1}\).
Подставляя \(\frac{KO}{OH_1} = \text{tg}(\phi)\) в выражение для \(\text{tg}(\theta)\), получаем окончательную формулу:
\(\text{tg}(\theta) = \text{cos}(\frac{180^\circ}{n}) \cdot \text{tg}(\phi)\).
Таким образом, тангенс угла \(\theta\) выражается через косинус угла \(\frac{180^\circ}{n}\) и тангенс угла \(\phi\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!