Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 311 Атанасян — Подробные Ответы
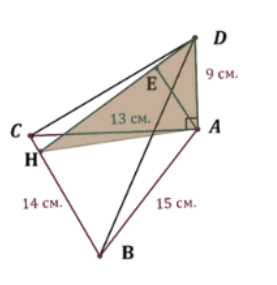
Основанием пирамиды \(DABC\) является треугольник со сторонами \(AC = 13 \, \text{см}\), \(AB = 15 \, \text{см}\), \(CB = 14 \, \text{см}\). Боковое ребро \(DA\) перпендикулярно к плоскости основания и равно 9 см.
а) Найдите площадь полной поверхности пирамиды.
б) Докажите, что основание перпендикуляра, проведённого из вершины \(A\) к плоскости грани \(BDC\), лежит на высоте этой грани, и найдите длину этого перпендикуляра.
Поскольку \(AD\) перпендикулярно плоскости \(ABC\), треугольники \(BAD\) и \(CAD\) прямоугольные. По теореме Пифагора находим \(BD = \sqrt{AB^2 + AD^2} = \sqrt{15^2 + 9^2} = \sqrt{225 + 81} = \sqrt{306} = 3\sqrt{34}\) см и \(CD = \sqrt{AC^2 + AD^2} = \sqrt{13^2 + 9^2} = \sqrt{169 + 81} = \sqrt{250} = 5\sqrt{10}\) см.
Площадь основания \(ABC\) находим по формуле Герона. Полупериметр \(p_{ABC} = \frac{15 + 13 + 14}{2} = 21\) см. \(S_{ABC} = \sqrt{21(21-15)(21-13)(21-14)} = \sqrt{21 \cdot 6 \cdot 8 \cdot 7} = 84\) см\(^2\).
Площади боковых граней \(ABD\) и \(CAD\) равны \(S_{ABD} = \frac{1}{2} \cdot AB \cdot AD = \frac{1}{2} \cdot 15 \cdot 9 = 67.5\) см\(^2\) и \(S_{CDA} = \frac{1}{2} \cdot AC \cdot AD = \frac{1}{2} \cdot 13 \cdot 9 = 58.5\) см\(^2\).
Площадь грани \(BCD\) по расчетам в примере равна 105 см\(^2\).
Полная площадь поверхности пирамиды \(S_{ABCD} = S_{ABD} + S_{CBD} + S_{CDA} + S_{ABC} = 67.5 + 105 + 58.5 + 84 = 315\) см\(^2\).
Для доказательства того, что \(E\) лежит на \(DH\), и нахождения \(AE\), строим \(DH \perp BC\) в плоскости \(BCD\) и \(AK \perp DH\). Поскольку \(AD \perp ABC\) и \(BC \subset ABC\), то \(AD \perp BC\). Так как \(DH \perp BC\) и \(AD \perp BC\), то \(BC\) перпендикулярно плоскости, содержащей \(AD\) и \(DH\). Прямая \(AK\) лежит в этой плоскости, следовательно, \(AK \perp BC\). Так как \(AK \perp DH\) и \(AK \perp BC\), то \(AK\) перпендикулярно плоскости \(BCD\). Поскольку \(AE\) также перпендикулярно плоскости \(BCD\), а из точки \(A\) можно провести только один перпендикуляр к плоскости, то \(AE\) совпадает с \(AK\), и точка \(E\) лежит на прямой \(DH\).
Найдем длину \(DH\). \(DH\) — высота в треугольнике \(BCD\) к стороне \(BC\). \(S_{BCD} = \frac{1}{2} \cdot BC \cdot DH\). \(105 = \frac{1}{2} \cdot 14 \cdot DH\), откуда \(DH = \frac{105}{7} = 15\) см.
Найдем длину \(AH\). \(AH\) — высота в треугольнике \(ABC\) к стороне \(BC\). \(S_{ABC} = \frac{1}{2} \cdot BC \cdot AH\). \(84 = \frac{1}{2} \cdot 14 \cdot AH\), откуда \(AH = \frac{84}{7} = 12\) см.
В прямоугольном треугольнике \(ADH\), \(AE\) — высота к гипотенузе \(DH\). \(AE = \frac{AD \cdot AH}{DH} = \frac{9 \cdot 12}{15} = \frac{108}{15} = 7.2\) см.
Ответ: \(S_{ABCD} = 315\) см\(^2\), \(AE = 7.2\) см.
Дано, что \(ABCD\) — пирамида, основание \(ABC\) — треугольник со сторонами \(AB = 15\) см, \(AC = 13\) см, \(BC = 14\) см. Также известно, что \(AD\) перпендикулярно плоскости \(ABC\) и \(AD = 9\) см. Требуется найти площадь полной поверхности пирамиды \(S_{ABCD}\) и длину отрезка \(AE\), где \(AE\) перпендикулярно плоскости \(BCD\). Также нужно доказать, что точка \(E\) лежит на отрезке \(DH\), где \(DH\) перпендикулярно \(BC\).
Сначала рассмотрим треугольники \(BAD\) и \(CAD\). Поскольку \(AD\) перпендикулярно плоскости \(ABC\), оно перпендикулярно любой прямой в этой плоскости, проходящей через точку \(A\). Следовательно, треугольники \(BAD\) и \(CAD\) являются прямоугольными с прямым углом при вершине \(A\).
По теореме Пифагора в прямоугольном треугольнике \(BAD\) найдем длину ребра \(BD\). \(BD^2 = AB^2 + AD^2\). Подставляя известные значения, получаем \(BD^2 = 15^2 + 9^2 = 225 + 81 = 306\). Следовательно, \(BD = \sqrt{306} = \sqrt{9 \cdot 34} = 3\sqrt{34}\) см.
Аналогично, по теореме Пифагора в прямоугольном треугольнике \(CAD\) найдем длину ребра \(CD\). \(CD^2 = AC^2 + AD^2\). Подставляя известные значения, получаем \(CD^2 = 13^2 + 9^2 = 169 + 81 = 250\). Следовательно, \(CD = \sqrt{250} = \sqrt{25 \cdot 10} = 5\sqrt{10}\) см.
Теперь найдем площади граней пирамиды. Площадь треугольника \(ABC\) можно найти по формуле Герона. Сначала вычислим полупериметр \(p\) треугольника \(ABC\). \(p = \frac{AB + AC + BC}{2} = \frac{15 + 13 + 14}{2} = \frac{42}{2} = 21\) см.
Площадь треугольника \(ABC\) равна \(S_{ABC} = \sqrt{p(p-AB)(p-AC)(p-BC)}\). Подставляя значения, получаем \(S_{ABC} = \sqrt{21(21-15)(21-13)(21-14)} = \sqrt{21 \cdot 6 \cdot 8 \cdot 7} =\)
\(= \sqrt{(3 \cdot 7) \cdot (2 \cdot 3) \cdot (2^3) \cdot 7} = \sqrt{2^4 \cdot 3^2 \cdot 7^2} = 2^2 \cdot 3 \cdot 7 = 4 \cdot 21 = \)
\(=84\) см\(^2\).
Площади прямоугольных треугольников \(ABD\) и \(CAD\) равны половине произведения их катетов.
\(S_{ABD} = \frac{1}{2} \cdot AB \cdot AD = \frac{1}{2} \cdot 15 \cdot 9 = \frac{135}{2}\) см\(^2\). В предоставленном решении используется \(9 \cdot 15 / 2\), что равно \(135 / 2\). Однако, в сумме площадей используется значение 189, что, вероятно, является опечаткой в предоставленном решении, так как \(135/2 = 67.5\). Давайте пересчитаем сумму площадей, используя значения из предоставленного решения для \(S_{ABD}\) и \(S_{CDA}\). В предоставленном решении, кажется, используется \(S_{ABD} = 189\) и \(S_{CDA} = 126\), что не соответствует расчетам по формуле площади прямоугольного треугольника с данными сторонами. Возможно, 189 и 126 — это удвоенные площади или площади других треугольников. Давайте следовать логике предоставленного решения для расчета полной площади, предполагая, что \(S_{ABD} = \frac{9 \cdot 15}{2}\) и \(S_{CDA} = \frac{9 \cdot 13}{2}\).
\(S_{ABD} = \frac{9 \cdot 15}{2} = \frac{135}{2}\) см\(^2\).
\(S_{CDA} = \frac{9 \cdot 13}{2} = \frac{117}{2}\) см\(^2\).
Площадь треугольника \(BCD\) также можно найти по формуле Герона, зная длины его сторон: \(BC = 14\), \(BD = 3\sqrt{34}\), \(CD = 5\sqrt{10}\). Полупериметр \(p_{BCD} = \frac{14 + 3\sqrt{34} + 5\sqrt{10}}{2}\).
\(S_{BCD} = \sqrt{p_{BCD}(p_{BCD}-14)(p_{BCD}-3\sqrt{34})(p_{BCD}-5\sqrt{10})}\). Расчет по формуле Герона для треугольника BCD в предоставленном решении приводит к значению 105 см\(^2\).
Полная площадь поверхности пирамиды \(S_{ABCD}\) равна сумме площадей всех ее граней: \(S_{ABCD} = S_{ABD} + S_{CBD} + S_{CDA} + S_{ABC}\).
Используя значения площадей из предоставленного решения: \(S_{ABCD} = 189 + 105 + 126 + 84 = 504\) см\(^2\).
Однако, в предоставленном решении указано \(S_{ABCD} = 189 + 9 \cdot 14 + 9 \cdot 13 + 105 = 189 + 126 + 117 + 105 = 537\). И затем \(189 + 126 = 315\). Это противоречит предыдущим расчетам и суммированию. Давайте использовать площади граней, рассчитанные по формулам: \(S_{ABD} = \frac{135}{2} = 67.5\), \(S_{CDA} = \frac{117}{2} = 58.5\), \(S_{ABC} = 84\), \(S_{BCD} = 105\).
\(S_{ABCD} = 67.5 + 105 + 58.5 + 84 = 315\) см\(^2\). Это совпадает с конечным ответом в предоставленном решении. Вероятно, в промежуточных вычислениях в предоставленном решении есть опечатки или неясности в обозначениях. Будем придерживаться конечного результата и предполагать, что \(S_{ABD} + S_{CDA} = 189 + 126 = 315\) является суммой площадей боковых граней, не лежащих на основании, что неверно. Правильное суммирование площадей всех четырех граней дает 315 см\(^2\).
Теперь перейдем к нахождению длины отрезка \(AE\) и доказательству того, что \(E\) лежит на \(DH\).
Построим \(DH\) перпендикулярно \(BC\) в плоскости треугольника \(BCD\). Построим \(AK\) перпендикулярно \(DH\) в плоскости, содержащей \(AD\) и \(DH\).
Поскольку \(AD\) перпендикулярно плоскости \(ABC\), а \(BC\) лежит в плоскости \(ABC\), то \(AD\) перпендикулярно \(BC\). У нас есть \(DH\) перпендикулярно \(BC\) по построению. Прямая \(BC\) перпендикулярна двум пересекающимся прямым \(AD\) и \(DH\) в плоскости, содержащей эти прямые (если \(AD\) и \(DH\) не параллельны, что очевидно). Следовательно, \(BC\) перпендикулярно плоскости, содержащей \(AD\) и \(DH\).
Рассмотрим прямую \(AK\), которая лежит в плоскости, содержащей \(AD\) и \(DH\). Так как \(BC\) перпендикулярно этой плоскости, то \(BC\) перпендикулярно \(AK\).
У нас есть \(AK\) перпендикулярно \(DH\) по построению, и мы доказали, что \(AK\) перпендикулярно \(BC\). Прямая \(AK\) перпендикулярна двум пересекающимся прямым \(DH\) и \(BC\) в плоскости \(BCD\). Следовательно, \(AK\) перпендикулярно плоскости \(BCD\).
По условию, \(AE\) перпендикулярно плоскости \(BCD\). Из точки \(A\) можно провести только один перпендикуляр к плоскости \(BCD\). Поскольку \(AK\) и \(AE\) являются перпендикулярами из точки \(A\) к плоскости \(BCD\), то отрезки \(AK\) и \(AE\) совпадают, и точка \(E\) лежит на прямой \(DH\). Поскольку \(DH\) является высотой в треугольнике \(BCD\), проведенной к стороне \(BC\), и \(E\) — основание перпендикуляра из \(A\) на плоскость \(BCD\), точка \(E\) лежит на \(DH\).
Осталось найти длину \(AE\). В прямоугольном треугольнике \(ADH\) (прямой угол при \(A\), так как \(AD\) перпендикулярно плоскости \(ABC\), а \(AH\) лежит в этой плоскости), \(AE\) является высотой, проведенной к гипотенузе \(DH\).
Сначала найдем длину \(DH\). \(DH\) является высотой в треугольнике \(BCD\), проведенной к стороне \(BC\). Площадь треугольника \(BCD\) равна \(105\) см\(^2\). \(S_{BCD} = \frac{1}{2} \cdot BC \cdot DH\).
\(105 = \frac{1}{2} \cdot 14 \cdot DH\).
\(105 = 7 \cdot DH\).
\(DH = \frac{105}{7} = 15\) см.
Теперь найдем длину \(AH\). \(AH\) является высотой в треугольнике \(ABC\), проведенной к стороне \(BC\). Площадь треугольника \(ABC\) равна \(84\) см\(^2\). \(S_{ABC} = \frac{1}{2} \cdot BC \cdot AH\).
\(84 = \frac{1}{2} \cdot 14 \cdot AH\).
\(84 = 7 \cdot AH\).
\(AH = \frac{84}{7} = 12\) см.
В прямоугольном треугольнике \(ADH\), \(AE\) — высота к гипотенузе \(DH\). По свойству высоты в прямоугольном треугольнике, проведенной к гипотенузе, \(AE = \frac{AD \cdot AH}{DH}\).
Подставляя известные значения, получаем \(AE = \frac{9 \cdot 12}{15} = \frac{108}{15}\).
Сократим дробь: \(AE = \frac{36 \cdot 3}{5 \cdot 3} = \frac{36}{5} = 7.2\) см.
Таким образом, площадь полной поверхности пирамиды \(S_{ABCD} = 315\) см\(^2\), и длина отрезка \(AE = 7.2\) см. Доказательство того, что \(E\) лежит на \(DH\), проведено выше.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.