Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 309 Атанасян — Подробные Ответы
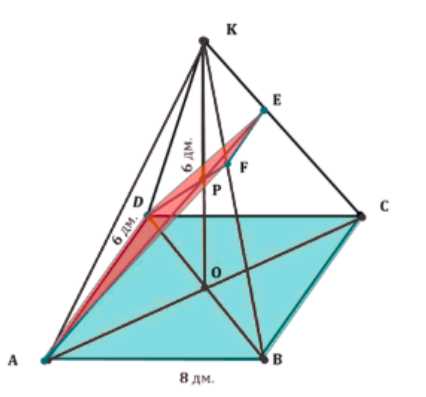
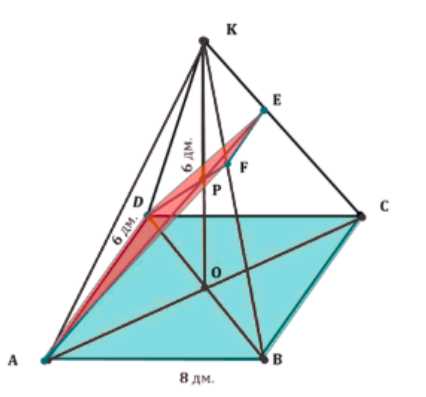
Основанием пирамиды с равными боковыми рёбрами является прямоугольник со сторонами 6 дм и 8 дм. Высота пирамиды равна 6 дм. Найдите площадь сечения, проведённого через меньшую сторону и середину высоты.
Применяя теорему Менелая к соответствующим треугольникам и секущим, получаем соотношения \(\frac{AP}{PE} = 3\) и \(\frac{DP}{PF} = 3\). Из подобия треугольников ADPA и AFPE следует, что \(\frac{EF}{AD} = \frac{PE}{AP} = \frac{PF}{DP} = \frac{1}{3}\). Таким образом, \(EF = \frac{AD}{3} = \frac{6}{3} = 2\) дм. Сечение DEFA является трапецией. Высота трапеции связана с высотой треугольника ADPA соотношением \(h_{DEFA} = \frac{4}{3} \cdot h_{ADPA}\). Высота \(h_{ADPA}\) находится из прямоугольного треугольника со сторонами 3 и 4 как \(h_{ADPA} = \sqrt{3^2 + 4^2} = 5\) дм. Следовательно, \(h_{DEFA} = \frac{4}{3} \cdot 5 = \frac{20}{3}\) дм. Площадь трапеции DEFA равна \(S_{DEFA} = \frac{1}{2} \cdot (AD + EF) \cdot h_{DEFA} = \frac{1}{2} \cdot (6 + 2) \cdot \frac{20}{3} = \frac{1}{2} \cdot 8 \cdot \frac{20}{3} = \frac{80}{3}\) дм².
Ответ: \(\frac{80}{3}\) дм².
Так как боковые грани пирамиды равны, то высота пирамиды КО опускается в центр основания.
Построим сечение, проходящее через точку Р. Проведем прямую АР. Точка Е является пересечением прямой АР и ребра КС, так как АР лежит в плоскости АКС. Аналогично, проведем прямую DP. Точка F является пересечением прямой DP и ребра КВ, так как DP лежит в плоскости DKB. Таким образом, сечение DEFA является искомым. Требуется найти площадь этого сечения.
Рассмотрим треугольник СКО и секущую ЕА. Применяя теорему Менелая к треугольнику СКО и секущей ЕА, получаем соотношение \(\frac{CE}{EK} \cdot \frac{KP}{PO} \cdot \frac{OA}{AC} = 1\). Из этого соотношения следует, что \(\frac{CE}{EK} = 2\).
Рассмотрим треугольник САЕ и секущую ОК. Применяя теорему Менелая к треугольнику САЕ и секущей ОК, получаем соотношение \(\frac{CO}{OA} \cdot \frac{AP}{PE} \cdot \frac{EK}{KC} = 1\). Из этого соотношения следует, что \(\frac{AP}{PE} = 3\). Обозначим это соотношение как (*).
Рассмотрим треугольник ВКО и секущую FD. Применяя теорему Менелая к треугольнику ВКО и секущей FD, получаем соотношение \(\frac{BF}{FK} \cdot \frac{KP}{PO} \cdot \frac{OD}{DB} = 1\). Из этого соотношения следует, что \(\frac{BF}{FK} = 2\).
Рассмотрим треугольник BDF и секущую ОК. Применяя теорему Менелая к треугольнику BDF и секущей ОК, получаем соотношение \(\frac{BO}{OD} \cdot \frac{DP}{PF} \cdot \frac{FK}{KB} = 1\). Из этого соотношения следует, что \(\frac{DP}{PF} = 3\). Обозначим это соотношение как (**).
Из соотношений (*) и (**) следует подобие треугольников DPA и FPE по пропорциональным сторонам и равным вертикальным углам. Из подобия следует соотношение сторон \(\frac{EF}{AD} = \frac{PE}{AP} = \frac{PF}{DP}\). Поскольку \(\frac{AP}{PE} = 3\), то \(\frac{PE}{AP} = \frac{1}{3}\). Аналогично, поскольку \(\frac{DP}{PF} = 3\), то \(\frac{PF}{DP} = \frac{1}{3}\). Следовательно, \(\frac{EF}{AD} = \frac{1}{3}\).
Далее находим длину отрезка EF. Из соотношения \(\frac{EF}{AD} = \frac{1}{3}\) и данного значения AD, получаем \(EF = \frac{AD}{3} = \frac{6}{3} = 2\) дм. Поскольку EF параллелен AD, сечение DEFA является трапецией.
Осталось найти высоту трапеции DEFA. Высота трапеции DEFA связана с высотой треугольника ADPA соотношением \(h_{DEFA} = \frac{4}{3} \cdot h_{ADPA}\). Это соотношение получено в силу подобия, доказанного ранее.
Для нахождения \(h_{ADPA}\) рассмотрим треугольник, образованный высотой \(h_{ADPA}\), высотой \(h_{AAOD}\) и отрезком РО. Этот треугольник является прямоугольным. Высота \(h_{AAOD}\), проведенная к стороне AD в прямоугольнике основания, равна половине стороны AB, то есть \(h_{AAOD} = \frac{AB}{2} = \frac{8}{2} = 4\) дм.
Высота \(h_{ADPA}\) находится как гипотенуза прямоугольного треугольника с катетами 3 и 4, то есть \(h_{ADPA} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\) дм.
Теперь найдем высоту трапеции DEFA: \(h_{DEFA} = \frac{4}{3} \cdot h_{ADPA} = \frac{4}{3} \cdot 5 = \frac{20}{3}\) дм.
Площадь трапеции DEFA вычисляется по формуле \(S_{DEFA} = \frac{1}{2} \cdot (AD + EF) \cdot h_{DEFA}\). Подставляя известные значения, получаем \(S_{DEFA} = \frac{1}{2} \cdot (6 + 2) \cdot \frac{20}{3} = \frac{1}{2} \cdot 8 \cdot \frac{20}{3} = 4 \cdot \frac{20}{3} = \frac{80}{3}\) дм².
Ответ: площадь сечения DEFA равна \(\frac{80}{3}\) дм².
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.