ГДЗ по Геометрии 10 класс Номер 307 Атанасян — Подробные Ответы

В правильной пирамиде \(MABCD\) \(AM = b\), \(AD = a\).
а) Постройте сечение пирамиды плоскостью \(\alpha\), проходящей через диагональ \(BD\) основания параллельно ребру \(MA\), и найдите площадь сечения.
б) Докажите, что точки \(M\) и \(C\) равноудалены от плоскости \(\alpha\).

Решение для правильной пирамиды \(ABCDM\) с квадратом \(ABCD\) (\(AD = a\)), где \(AM = b\), а \(O\) — центр основания.

а) Сечение через \(BD\), параллельное \(MA\):
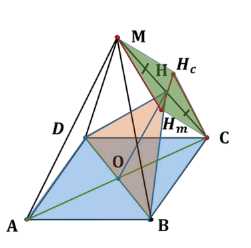
1. Находим середину \(MC\) — точку \(H\).
2. \(OH\) — средняя линия \(\triangle ACM\), значит \(OH \parallel AM\) и \(OH = \frac{b}{2}\).
3. Искомое сечение — плоскость \(BHD\), так как \(BD \in BHD\) и \(OH \parallel AM\).
4. Площадь сечения:
\(
S_{BHD} = \frac{1}{2} \cdot BD \cdot OH = \frac{a b \sqrt{2}}{4}.
\)

б) Равноудаленность \(M\) и \(C\) от \(BHD\):
1. Проводим перпендикуляры \(MH_m\) и \(CH_c\) к плоскости \(BHD\).
2. Из равенства прямоугольных треугольников \(MHH_m\) и \(CHH_c\) (по гипотенузе и углу) следует \(MH_m = CH_c\).

Ответ:
\(
S_{BHD} = \frac{a b \sqrt{2}}{4}.
\)
Точки \(M\) и \(C\) равноудалены от плоскости сечения.

Решение задачи о правильной пирамиде \(ABCDM\) с квадратом \(ABCD\) в основании и вершиной \(M\), где \(AM = b\), \(AD = a\), а \(O\) — центр квадрата.

а) Построим сечение через \(BD\), параллельное \(MA\).

1. Найдем середину \(H\) отрезка \(MC\): \(MH = HC\).
2. Поскольку \(O\) — центр квадрата, \(O\) является серединой \(AC\).
3. Отрезок \(OH\) — средняя линия треугольника \(ACM\), поэтому \(OH \parallel AM\) и \(OH = \frac{1}{2} AM = \frac{b}{2}\).
4. Так как \(OH \parallel AM\), а сечение должно быть параллельно \(AM\), то плоскость сечения проходит через \(BD\) и параллельна \(OH\).
5. Таким образом, сечение — это плоскость \(BHD\), где \(H\) лежит на \(MC\).

Докажем, что \(BHD\) — искомое сечение:
— \(BD\) лежит в плоскости сечения.
— \(OH \parallel AM\), а \(OH\) лежит в плоскости \(BHD\), следовательно, \(AM \parallel BHD\).

Площадь сечения \(BHD\):
— Диагональ квадрата \(BD = a\sqrt{2}\).
— Высота \(OH = \frac{b}{2}\).
— Площадь треугольника \(BHD\):
\(
S_{BHD} = \frac{1}{2} \cdot BD \cdot OH = \frac{1}{2} \cdot a\sqrt{2} \cdot \frac{b}{2} = \frac{a b \sqrt{2}}{4}.
\)

б) Докажем, что точки \(M\) и \(C\) равноудалены от плоскости \(BHD\).

1. Проведем перпендикуляры из \(M\) и \(C\) к плоскости \(BHD\): \(MH_m\) и \(CH_c\).
2. Так как \(AM \parallel BHD\), а \(MH_m\) и \(CH_c\) перпендикулярны \(BHD\), то \(MH_m \parallel CH_c\) и лежат в одной плоскости.
3. Рассмотрим треугольники \(MHH_m\) и \(CHH_c\):
— \(MH = HC\) (по построению).
— Углы при \(H\) равны (вертикальные).
— Углы \(MH_mH\) и \(CH_cH\) прямые.
4. Следовательно, треугольники равны по гипотенузе и острому углу, откуда \(MH_m = CH_c\).

Ответ:
\(
S_{BHD} = \frac{a b \sqrt{2}}{4}.
\)
Точки \(M\) и \(C\) равноудалены от плоскости сечения.