
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 304 Атанасян — Подробные Ответы
В правильной четырёхугольной пирамиде плоский угол при вершине равен \(60^\circ\). Докажите, что двугранный угол между боковой гранью и основанием пирамиды вдвое меньше двугранного угла при боковом ребре.
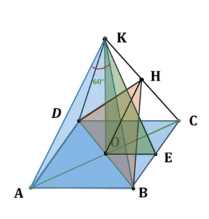
Дано: \(ABCDK\) — правильная пирамида, \(\angle AKB = 60^\circ\). Доказать: \(\angle BKCD = 2 \cdot \angle ABCK\).
Так как \(\triangle AKB\) равносторонний, все рёбра равны (\(AB = AK = BK = x\)). Из центра \(O\) квадрата \(ABCD\) проведём перпендикуляры \(OH\) и \(OE\) к \(AK\) и \(BC\).
В прямоугольных \(\triangle OHB\) и \(\triangle OEK\):
— \(OE = \frac{x}{2}\) (половина стороны квадрата),
— \(OH = \frac{x}{2}\) (по теореме Фалеса, так как \(AK \parallel KC\) и \(O\) — середина \(AC\)).
Так как \(KE = HB\) (высоты в равных \(\triangle BKC\)), то \(\triangle OHB \cong \triangle OEK\) по гипотенузе и катету. Следовательно, \(\angle OHB = \angle OEK\).
В равнобедренном \(\triangle DHB\) медиана \(HO\) — биссектриса, поэтому:
\(\angle BKCD = 2 \cdot \angle OHB = 2 \cdot \angle ABCK.\)
Дано: \(ABCDK\) — правильная пирамида, \(ABCD\) — квадрат, \(\angle AKB = 60^\circ\), \(O\) — центр квадрата. Требуется доказать: \(\angle BKCD = 2 \cdot \angle ABCK\).
По условию \(\triangle AKB\) — равнобедренный с углом при вершине \(60^\circ\), значит, он равносторонний. Следовательно, все грани пирамиды — равные равносторонние треугольники, и все рёбра равны. Обозначим длину ребра за \(x\).
Из центра основания \(O\) проведём высоты к соответствующим сторонам. По построению и свойствам правильной пирамиды, полученные углы \(\angle DHB\) и \(\angle OEK\) являются линейными двугранными углами соответственно для \(\angle BKCD\) и \(\angle ABCK\).
Рассмотрим прямоугольные треугольники \(\triangle OHB\) и \(\triangle OEK\):
— \(OE = \frac{AB}{2} = \frac{x}{2}\), так как \(ABCD\) — квадрат.
— \(\triangle AKC\) — прямоугольный по теореме, обратной теореме Пифагора: \(AK^2 + KC^2 = x^2 + x^2 = (\sqrt{2} \cdot x)^2 = AC^2\) (диагональ квадрата).
— По построению \(OH \perp AK\), поэтому по теореме Фалеса \(OH = \frac{KC}{2} = \frac{x}{2} = OE\).
В треугольнике \(\triangle BKC\) все высоты равны, поэтому \(KE = HB\). Из равенства \(OH = OE\) и \(KE = HB\) следует, что \(\triangle OHB\) и \(\triangle OEK\) равны по гипотенузе и катету. Следовательно, \(\angle OHB = \angle OEK\).
Учитывая, что \(\triangle DHB\) — равнобедренный, медиана \(HO\) является биссектрисой, поэтому: \(\angle OHB = \frac{1}{2} \cdot \angle DHB = \angle OEK.\) Таким образом, \(\angle BKCD = 2 \cdot \angle ABCK\), что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!