ГДЗ по Геометрии 10 класс Номер 303 Атанасян — Подробные Ответы

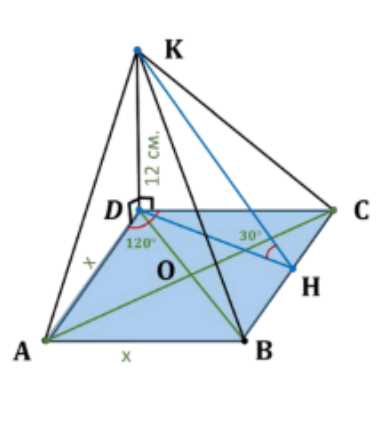
Основанием пирамиды является ромб. Две боковые грани перпендикулярны к плоскости основания и образуют двугранный угол в \(120^\circ\), а две другие боковые грани наклонены к плоскости основания под углом в \(30^\circ\). Найдите площадь поверхности пирамиды, если её высота равна 12 см.

Дано: пирамида \(ABCDK\) с ромбом \(ABCD\) в основании, \(AKD \perp ABC\), \(CKD \perp ABC\), \(KD = 12\,\text{см}\), \(\angle KABD = 30^\circ\), \(\angle AKDC = 120^\circ\). Найти полную поверхность \(S_{ABCDK}\).

Решение:
1. Так как \(ABCD\) — ромб и \(\angle ADC = 120^\circ\), то \(\angle DAB = 60^\circ\), а треугольники \(\triangle ABD\) и \(\triangle ABC\) — равносторонние.
2. Из условия \(DK \perp ABC\) находим высоту \(KH\) треугольника \(ABK\):
\(KH = \frac{DK}{\sin 30^\circ} = 24\,\text{см}\)
3. Сторона ромба \(x\) определяется через высоту \(h = 12\sqrt{3}\,\text{см}\):
\(x = \frac{2h}{\sqrt{3}} = 24\,\text{см}\)
4. Площади граней:
— Основание: \(S_{ABCD} = 288\sqrt{3}\,\text{см}^2\)
— Боковые грани: \(S_{ABK} = S_{BCK} = 288\,\text{см}^2\), \(S_{ADK} = S_{CDK} = 144\,\text{см}^2\)
5. Полная поверхность:
\(S_{ABCDK} = 288\sqrt{3} + 864\,\text{см}^2\)

Ответ: \(S_{ABCDK} = 288\sqrt{3} + 864\,\text{см}^2\).

Дано: \(ABCDK\) — пирамида, \(ABCD\) — ромб, \(AKD \perp ABC\), \(CKD \perp ABC\), \(KD = 12\,\text{см}\), \(\angle KABD = 2 \cdot \angle KCBD = 30^\circ\), \(\angle AKDC = 120^\circ\), \(O\) — центр пересечения диагоналей.

Найти: \(S_{ABCDK}\) — полную поверхность пирамиды.

По построению \(\angle ADC = 120^\circ\) (линейный угол двугранного угла). Так как \(ABCD\) — ромб, то \(\angle DAB = 60^\circ\), а треугольники \(\triangle ABD\) и \(\triangle ABC\) — равносторонние. Обозначим сторону ромба за \(x\).

Так как \(DK \perp ABC\) (из условий \(AKD \perp ABC\) и \(CKD \perp ABC\)), то \(DK\) — высота пирамиды. Для прямоугольного треугольника \(\triangle KDH\) (где \(DH\) — проекция \(KH\) на плоскость \(ABC\)):

\(KH = \frac{DK}{\sin 30^\circ} = \frac{12}{0.5} = 24\,\text{см}\)

\(DH = KH \cdot \cos 30^\circ = 24 \cdot \frac{\sqrt{3}}{2} = 12\sqrt{3}\,\text{см}\)

В равностороннем треугольнике \(\triangle ABD\) высота \(h\) равна:

\(h = \frac{x \sqrt{3}}{2}\)

Но \(DH\) — это расстояние от точки \(D\) до плоскости \(ABK\), и оно совпадает с высотой ромба. Таким образом:

\(h = 12\sqrt{3}\,\text{см}\)

Отсюда находим сторону ромба \(x\):

\(x = \frac{2h}{\sqrt{3}} = \frac{2 \cdot 12\sqrt{3}}{\sqrt{3}} = 24\,\text{см}\)

Теперь вычислим площади всех граней пирамиды:

1. Площадь основания \(ABCD\) (ромб):

\(S_{ABCD} = x^2 \cdot \sin 60^\circ = 24^2 \cdot \frac{\sqrt{3}}{2} = 288\sqrt{3}\,\text{см}^2\)

2. Площадь боковой грани \(ABK\):

Так как \(DK \perp ABC\), то высота треугольника \(ABK\) равна \(KH = 24\,\text{см}\). Тогда:

\(S_{ABK} = \frac{1}{2} \cdot AB \cdot KH = \frac{1}{2} \cdot 24 \cdot 24 = 288\,\text{см}^2\)

3. Аналогично для грани \(BCK\):

\(S_{BCK} = 288\,\text{см}^2\)

4. Для грани \(CDK\):

Высота равна \(DK = 12\,\text{см}\), так как \(DK \perp ABC\) и \(CD\) лежит в плоскости \(ABC\):

\(S_{CDK} = \frac{1}{2} \cdot CD \cdot DK = \frac{1}{2} \cdot 24 \cdot 12 = 144\,\text{см}^2\)

5. Для грани \(ADK\):

\(S_{ADK} = 144\,\text{см}^2\)

Теперь найдём полную поверхность пирамиды:

\(S_{ABCDK} = S_{ABCD} + S_{ABK} + S_{BCK} + S_{CDK} + S_{ADK} =\)
\(= 288\sqrt{3} + 288 + 288 + 144 + 144\)

\(S_{ABCDK} = 288\sqrt{3} + 864\,\text{см}^2\)

Ответ: \(S_{ABCDK} = 288\sqrt{3} + 864\,\text{см}^2\).