
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 302 Атанасян — Подробные Ответы
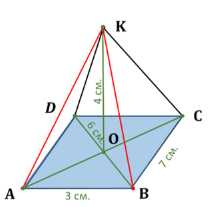
Основанием пирамиды является параллелограмм со сторонами 3 см и 7 см и одной из диагоналей 6 см. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 4 см. Найдите боковые рёбра пирамиды.
Краткое решение:
Дано: \(ABCDK\) — пирамида, \(ABCD\) — параллелограмм с \(AB = 3\) см, \(BC = 7\) см, \(BD = 6\) см, \(KO = 4\) см (\(O\) — центр диагоналей).
1. Находим \(KB\) по теореме Пифагора:
\(KB = \sqrt{KO^2 + OB^2} = \sqrt{4^2 + 3^2} = 5 \text{ см}\)
2. Находим \(OC\) через теорему косинусов для \(\triangle COB\):
\(49 = CO^2 + 9 — 6 \cdot CO \cdot \cos(\angle COB)\)
\(CO = \sqrt{20} = 2\sqrt{5} \text{ см}\)
3. Находим \(KC\) по теореме Пифагора:
\(KC = \sqrt{4^2 + (2\sqrt{5})^2} = 6 \text{ см}\)
Ответ: \(KB = KD = 5\) см, \(KC = KA = 6\) см.
Решение задачи о нахождении боковых ребер пирамиды \(ABCDK\):
Дано: \(ABCDK\) — пирамида, \(ABCD\) — параллелограмм, \(AB = 3\) см, \(BC = 7\) см, \(BD = 6\) см, \(KO = 4\) см, где \(O\) — центр пересечения диагоналей параллелограмма.
В силу симметрии ребра пирамиды попарно равны: \(AK = KC\), \(BK = KD\). Так как в параллелограмме точка пересечения диагоналей делит их пополам, то \(OD = OB = \frac{BD}{2} = 3\) см.
Найдем \(KB\) по теореме Пифагора для прямоугольного треугольника \(KOB\):
\(KB = \sqrt{KO^2 + OB^2} = \sqrt{4^2 + 3^2} = \sqrt{16 + 9} = 5 \text{ см}\)
Для нахождения \(AO\) и \(OC\) воспользуемся теоремой косинусов для треугольника \(AOB\):
\(AB^2 = AO^2 + OB^2 — 2 \cdot AO \cdot OB \cdot \cos(\angle AOB)\)
\(3^2 = AO^2 + 3^2 — 2 \cdot AO \cdot 3 \cdot \cos(\angle AOB)\)
\(9 = AO^2 + 9 — 6 \cdot AO \cdot \cos(\angle AOB)\)
\(AO^2 = 6 \cdot AO \cdot \cos(\angle AOB)\)
Так как \(\angle AOB\) и \(\angle COB\) — смежные углы, то \(\cos(\angle AOB) = -\cos(\angle COB)\).
Применим теорему косинусов для треугольника \(COB\):
\(CB^2 = CO^2 + OB^2 — 2 \cdot CO \cdot OB \cdot \cos(\angle COB)\)
\(7^2 = CO^2 + 3^2 — 2 \cdot CO \cdot 3 \cdot \cos(\angle COB)\)
\(49 = CO^2 + 9 — 6 \cdot CO \cdot \cos(\angle COB)\)
\(40 = CO^2 — 6 \cdot CO \cdot \cos(\angle COB)\)
Подставим \(\cos(\angle COB) = -\frac{AO}{6}\) (из предыдущего уравнения):
\(40 = CO^2 — 6 \cdot CO \cdot \left(-\frac{AO}{6}\right)\)
\(40 = CO^2 + CO \cdot AO\)
Так как \(AO = OC\) (по свойству параллелограмма), то:
\(40 = 2 \cdot CO^2\)
\(CO^2 = 20\)
\(CO = \sqrt{20} = 2\sqrt{5} \text{ см}\)
Теперь найдем \(KC\) по теореме Пифагора для прямоугольного треугольника \(KOC\):
\(KC = \sqrt{KO^2 + OC^2} = \sqrt{4^2 + (2\sqrt{5})^2} = \sqrt{16 + 20} = 6 \text{ см}\)
Ответ: \(KB = KD = 5\) см, \(KC = KA = 6\) см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!